filmov
tv
Sum of four Squares
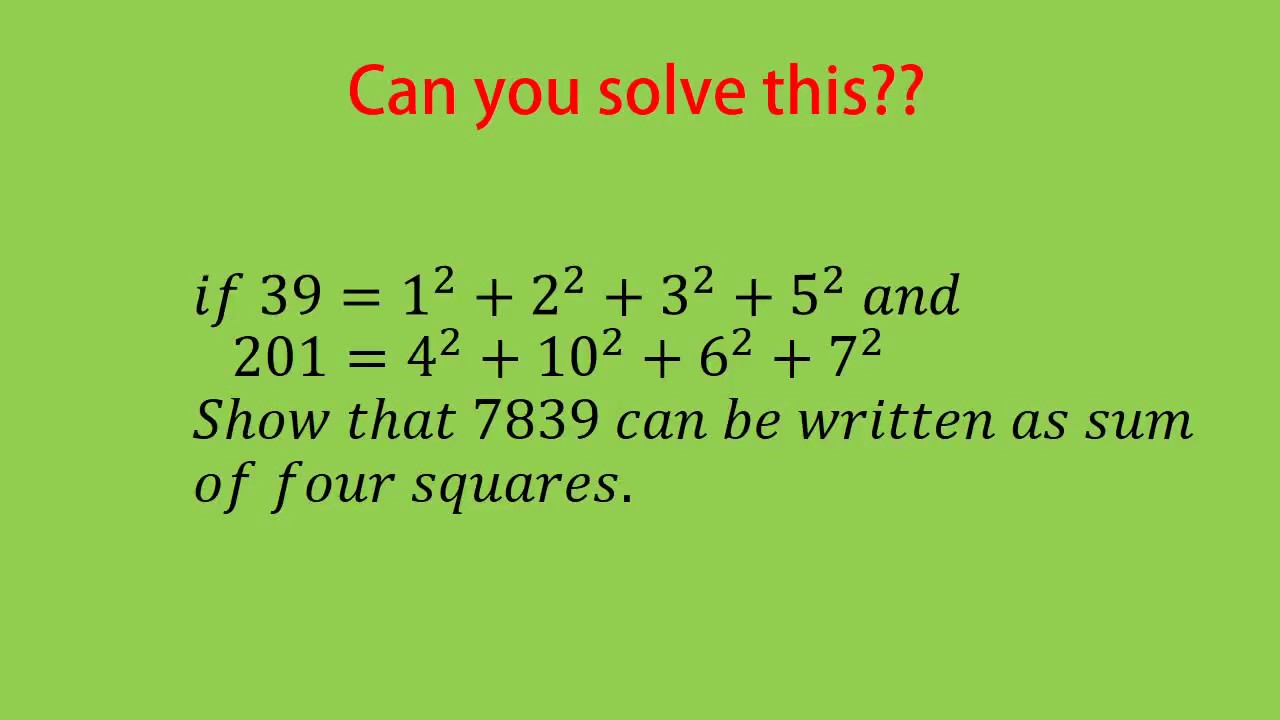
Показать описание
In this video you will learn that if and two integer can be written as sum of two squares their product can also be written as the sum of squares of four integers using Euler's identity. The proof of Euler's identity is simple algebraic manipulation that even a 8th grader can do!
Writing Numbers as the Sum of Four Squares
Sum of Four Squares
Sum of four Squares
11 2 Sums of Four Squares
Any natural number can be written as the sum of four squares
Sum of four squares | BSC MATH |
Finding the sum of four squares
Number Theory | Sums of squares: Part 6.
IMO Class 4 2021-22 Set B | International Maths Olympiad Class 4
2023 Number Challenge: Find sum of four squares that is equal to 2023
Number Theory | Sums of Squares Part 1.
2020 As Sum of Four Squares
Number Theory | Sums of Squares Part 7.
521 Math #129: Sum of squares of four smallest factors (Number theory question from SMO(J) 2018)
#1 What's so interesting about squared numbers? Lagrange’s Four Square Theorem
Summing Squares in a Rectangle
Sum of squares of four consecutive integers is 630 Solve by Factoring
Sums of Squares and Golden Gates - Peter Sarnak (Princeton)
🧩Math Oddity: All +integers sum of 4 perfect squares #shorts #youtubeshorts #subscribe #motivational...
The Sum Of The Area Of Four Squares is 2019, Then What Would Be The Area Of The Red Rectangle ?
Jacobi's four-square theorem
Sum of n squares | explained visually |
Sums of Squares and Gaussian integers: Part 4
Common mistake in prime factorization | What is the sum of four integers?
Комментарии
 0:01:59
0:01:59
 0:15:19
0:15:19
 0:01:33
0:01:33
 0:06:15
0:06:15
 0:00:28
0:00:28
 0:07:39
0:07:39
 0:01:41
0:01:41
 0:06:05
0:06:05
 0:30:14
0:30:14
 0:00:45
0:00:45
 0:06:37
0:06:37
 0:00:20
0:00:20
 0:20:11
0:20:11
 0:09:23
0:09:23
 0:01:19
0:01:19
 0:01:00
0:01:00
 0:05:48
0:05:48
 1:05:51
1:05:51
 0:00:16
0:00:16
 0:02:39
0:02:39
 0:01:07
0:01:07
 0:02:14
0:02:14
 0:21:47
0:21:47
 0:03:31
0:03:31