filmov
tv
Abstract Algebra 78: The ring of Gaussian integers
Показать описание
Abstract Algebra 78: The ring of Gaussian integers
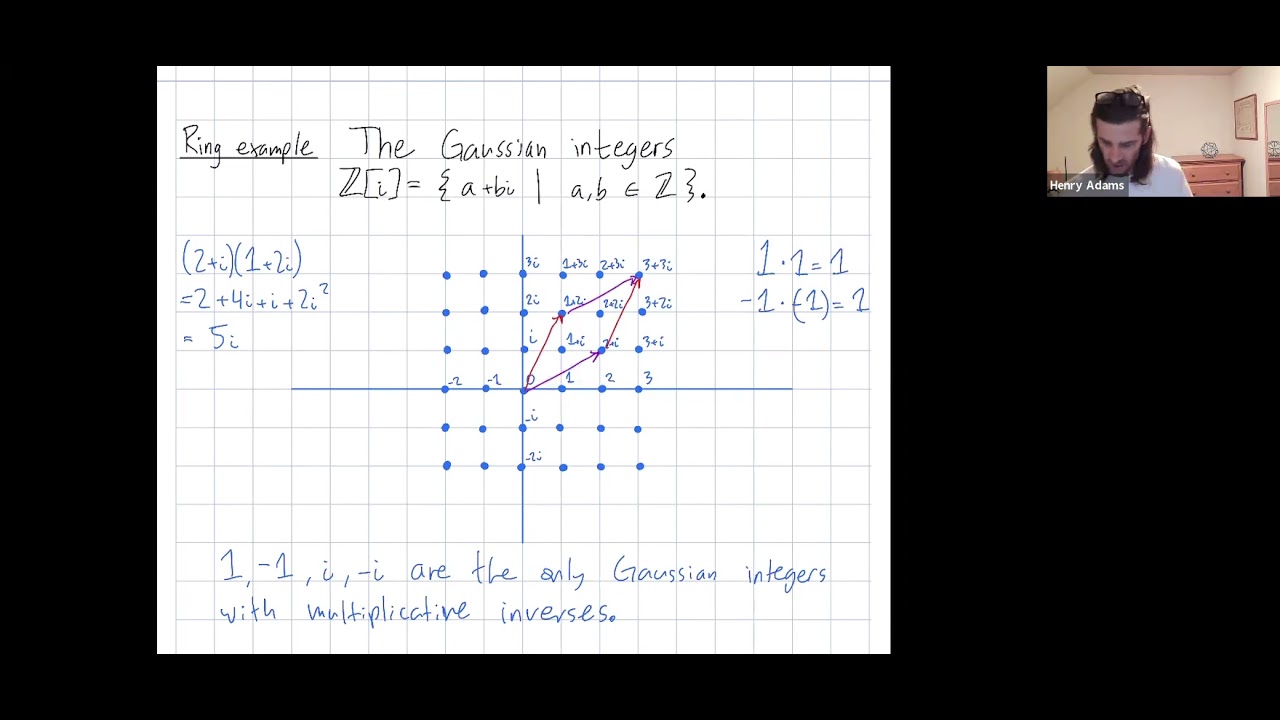
Abstract: The Gaussian integers are all complex numbers which have both an integer real part and an integer imaginary part. We describe with the Gaussian integers form a ring. We also discuss why the only Gaussian integers that have multiplicative inverses are 1, -1, i, and -i.
This video accompanies the class "Introduction to Abstract Algebra" at Colorado State University:
Abstract: The Gaussian integers are all complex numbers which have both an integer real part and an integer imaginary part. We describe with the Gaussian integers form a ring. We also discuss why the only Gaussian integers that have multiplicative inverses are 1, -1, i, and -i.
This video accompanies the class "Introduction to Abstract Algebra" at Colorado State University:
0:16:02
Abstract Algebra 78: The ring of Gaussian integers
0:17:45
Abstract Algebra | Some basic exercises involving rings.
0:36:29
Abstract Algebra 29A: Visualize Factor Rings of Gaussian Integers Z[i], Construct Complex Field C
0:00:05
In Abstract Algebra, In Ring, Ideal is special type of subring. like and Subscribe for more info
0:14:15
Abstract Algebra 77: Subrings
0:00:11
#simplification #tricks
0:14:09
45 The ring Z/nZ (part 5)
0:34:45
Irreducible Polynomials
0:05:32
Gaussian Integers
0:18:10
What is...a ring?
0:13:36
78 Product of two arbitrary polynomials Notation
0:48:38
Ring Theory | Examples | Gaussian Integer | Abstract Algebra
0:13:24
Ring Homomorphisms
0:00:16
Most💯 Important Step Before any Procedure 🔥
0:03:51
Solving congruences, 3 introductory examples
0:40:52
Abstract Algebra: The Ring-Part(vi):By Dr P R PARIHAR
0:11:02
# 6 Gaussian Integer Ring Theory (Abstract Algebra)
0:50:01
Group Theory: 02 Introduction to Abstract Algebra
0:05:12
Solution |Que.77-78; Chapter-3; Contemporary Abstract Algebra-8th Ed. | Joseph A. Gallian| Subgroups
0:00:13
Indian vs Japanese Maths 🔥| Vedic Maths Trick for Fast Calculation | Speed Maths #trending #shorts...
0:08:03
Rings, Boolean ring is commutative ring
0:05:24
78 Number Systems for Analysis Oct 2023 Mendelson Ch 1 Reading
0:20:32
Abstract Algebra : Module 4 Section 24 Part 2 Group Ring
0:25:31
Abstract Algebra | Every PID is a UFD.
Комментарии