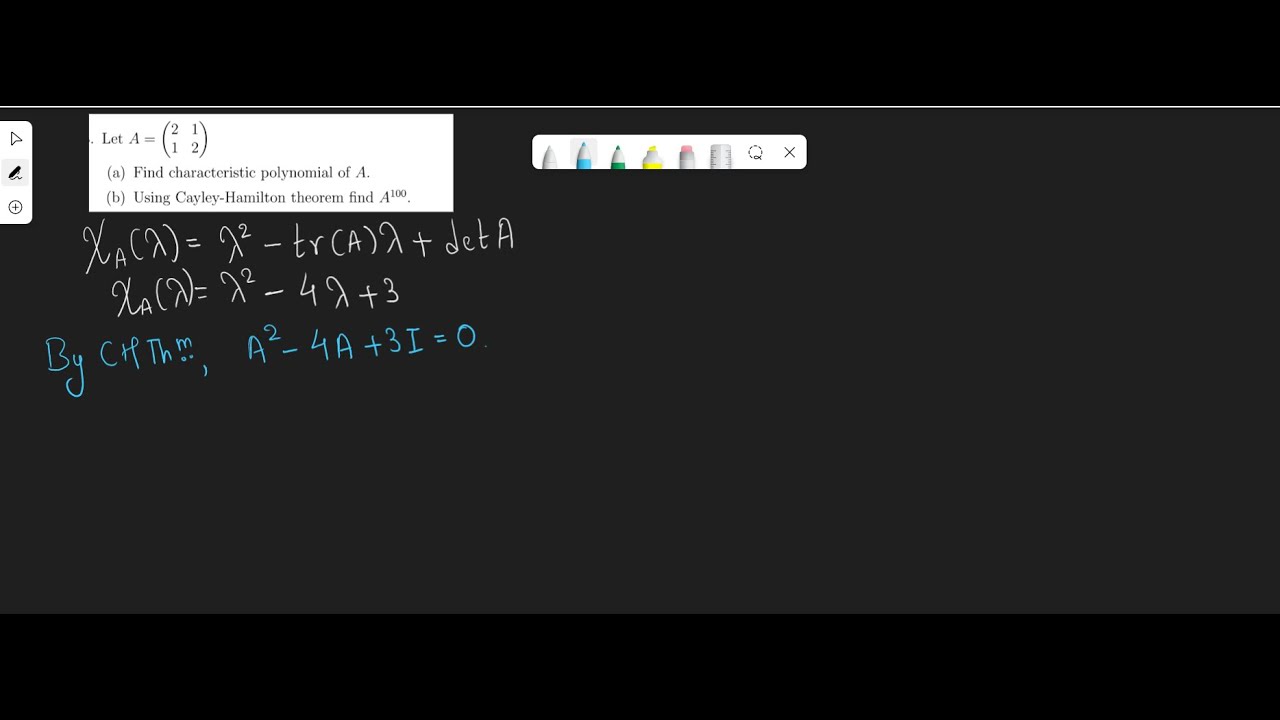
Find A^100 if A^2-4A+3I=0| Cayley Hamilton theorem| Linear Algebra

Welcome to our channel exploring the powerful Cayley-Hamilton Theorem in linear algebra! In this video, we delve into an intriguing problem: determining A^100 when given that A^2 - 4A + 3I = 0,where A is a square matrix and I is the identity matrix.

Join us on an illuminating journey as we employ the Cayley-Hamilton Theorem to solve this problem step-by-step. This theorem asserts that every square matrix satisfies its own characteristic equation. We'll demonstrate how this theorem enables us to manipulate the given equation involving A to find a polynomial equation satisfied by A, thus allowing us to compute higher powers of A without direct matrix multiplication.

Through detailed explanations, practical examples, and an intuitive breakdown of the theorem's application, we'll showcase how the Cayley-Hamilton Theorem provides a powerful shortcut for computing higher powers of matrices with given relations.

Whether you're a student navigating linear algebra coursework or someone fascinated by the elegance of mathematical theorems, this video offers valuable insights into the Cayley-Hamilton Theorem's application.

Subscribe now for a comprehensive understanding of this theorem! Join us as we unlock the elegance and utility of the Cayley-Hamilton Theorem, solving problems and unraveling the mysteries of matrix algebra. Dive into proof explanations and problem-solving strategies that will enhance your grasp of linear algebraic concepts!

Write in the comment section for the topic of your choice to start with.
Also for any other doubt and difficulties be free to ask in comment section.
Thank You.
#jam #IIT #realanalysis #sequence #sagarjagad #GATE #mathematics