Learn Reactive Power in AC Circuits - Reactive Power Inductive Load and Power Factor Calculation

In this lesson you will learn about power analysis in AC circuit analysis. Here we discuss Reactive power with an inductive Load. We will learn how the energy from the circuit is stored in the magnetic field of the inductor and later in the cycle the energy is extracted from the magnetic field. The student will learn the difference between real and reactive power. We will also discuss how reactive power is involved in power factor calculations.

-----------------------

hello welcome to this lesson in AC
circuit analysis.

the title of this
lesson is called reactive power with an
inductive load so we're going to talk
about the concept of reactive power here
and we're going to be talking about the
concept when that applies to having an
inductor inside of the load.

and the last
section we had just a resistive Network
just resistors and we talked to in great
detail about what's going on with the
power when we just have resistors so if
you haven't watched that section go back
and watch it and you to reacquaint
yourself what's happening with resistive
Network is we have an a nonzero average
we have an average amount of power
delivered to that resistor and the it's
it's oscillating the instantaneous power.

is oscillating up and down but it's
always positive and so there's always an
average value when you have a resistive
Network here we'll talk about what
happens we have inductive loads the next
section we'll talk about what happens we
have capacitive loads really excited to
teach this because up until now we talk
about resistors everyone can wrap your
brain around resistors right because
resistors are kind of the easiest thing
to understand circuits they obey Ohm's
law is equal to IR and you have some
kind of familiarity with with what's
going to happen when the sinusoids go up
and down and things are in phase you.

know the current the voltage are in
phase so it's kind of even though there
was a lot of math in the last section it
was very easy to follow i think if you
watch it enough times and study it
enough times what's really happening
with a resistor but when you have
inductors and when you have capacitor
suddenly the current and the voltage
across those things are no longer in
phase and things get a little bit murky
so we're going to take it slow
we're not doing problems are going to
theory for the next few sections and
when you get to your problems you'll
understand these terms you'll understand
what's really happening
so let's revisit this is what I call the
granddaddy power equation i'm going to
leave it on the board for very for a
great many sections its instantaneous
power so if you start the stopwatch and
time marches on this is the time
dependence here this is a constant term
these this is the time dependence you
stick in the numbers with your phase
angles for the current the voltage which
is going to be governed by your circuit
that you have and this is going to be
some kind of sinusoid overtime and it's
telling you that the instantaneous power
is always changing but we want to zero
in on the case when we have just an
inductive load what's going to happen
when there's just an end.

after inside the box last section we
talked about what happens when there's a
capacitor in the box now we're going to
talk about if the load is purely
inductive what happens and i can tell
you right now actually it's something
really cool that happens and I i find
this stuff really fascinated with
circuit analysis so this is some of the
reasons i'm really excited about
teaching it right the first thing you
need to remember there's very very few
things I tell you in circuit theory to
just remember right one of them's Ohm's
law is equal to IR right you have to
know that some of the real basic power
equations just memorize them what I'm
going to tell you here is something you
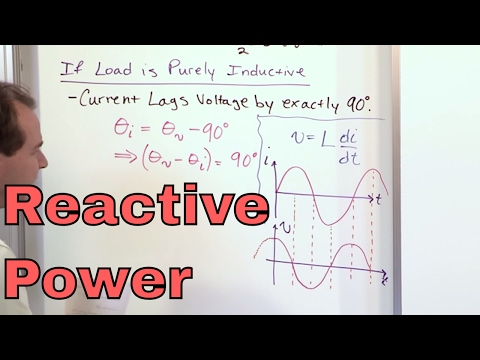
should just remember when you have a
purely inductive load all right
the current ok crossing through that
inductor lags the voltage by 90 degrees
exactly the current lags the voltage and
an inductor or across an inductor by
exactly 90 degrees current lags the
voltage by 90 degrees i'm going to show
you how to prove that to yourself but
just remember it because if you can just
remember it that these few little things
I tell you to remember it's going to
make your life so much easier
so let's go down here and write that
down and I'll explain what i'm talking
about the current lags the voltage by
I'm gonna put the word exactly 90
degrees and i'll give you a hint when we
get two capacitors it's also going to be
90 degrees but the current is not gonna
lag the voltage a capacitor the current
will lead the voltage by 90 degrees so
the 90 degrees part is going to be easy
to remember the leading versus the
lagging is what always confused me when.

[zuhairalsaffar]

Sir, you have done this subject as easy as possible for me and for my friends so, you deserve a great thank 🎉🎉🎉❤

[jacobvandijk]

After 2:51: Just remember the word CIVIL: for a capacitor C the current (I) leads the voltage (V), but the voltage (V) leads the current (I) for an inductor L.

[bernardocisneros]

Great explanation and illustration of how the voltage across an inductor is related to the rate of change in current through it and not the magnitude of the current.

[GebzNotJebz]

i have very mixed feelings about this channel, very happy that someone puts that much effort into videos and the overall quality of the content, and really sad that it doesn't get the amount of recognition it deserves..
Either way.. Cheers, good stuff!

[shaneglynn]

Hello, I'm just after finding you and your videos. I'm wondering if there's any chance you can make some kinda playlist with all of your electronics videos please. Finding it difficult to find them amongst everything else.

[LeopoldoYoshioka]

Excellent explanation about power behavior in the inductor. It is a difficult concept to learn alone in the books. Thank very much.

[fredboxberger]

The Army also taught us to visualize a cap as a short as electrons rush in to charge it as E increases. And magnetic flux resists electron flow in L, as E rises. Never forgot that either.

[ZmannR]

Or just remember "ELI the ICE man". Therefore voltage leads current in inductive and current leads voltage in capacitive circuits.

[masiurrahman]

He should write a book.
How accurate his explanation is!!

[bhupessarkar]

I am really enriched viewing the lecture.

[nateknowsmore]

Nothing like a good you tube video first thing in the morning to make me feel like an idiot...going to be a great day

[fredboxberger]

The Army taught us it is ELI the ICE man! E leads I in an L circuit. I leads E in a C circuit! Learned that 50 years ago. Never forgot it.

[manicsurfing]

Thank you for this
Two quick questions:
- would a bifoilar coil connected continuous to itself with a stored magnetic field be likened to an inductor or capacitor? Hopefully I asked that correctly
-also you look similar to the fella that has the majorprep channel and thought emporium is there relation? Thanks for your time and efforts

[soldatheero]

Can someone help answer and explain this question?

A coil and a capacitor are connected in series across a 120v. The coil has an impedance of 232 Ohms at a p.f of 81deg lagging. The capacitive reactance of the capacitor is 150 ohms. Calculate the V across the coil and voltage across the capacitor.

[brianmcdonough]

Hello,



This comment is kind of a hail mary, but I figured I’d try. I’m working for a consulting firm where I am beginning to do electrical engineering tasks (I am a mech eng graduate). One concept is bothering me – in my circuit textbook it often describes in a problem how I am “delivering” 80 W of power and “absorbing” 60 VAR of magnetizing power. It then says that my overall complex power has a magnitude of 100VA. Maybe it’s a language interpretation but if I am “delivering” but also “absorbing” why do I still need to provide more apparent power? Doesn’t “absorb” imply that I am being “helped” by the magnetizing VARs? This is for a capacitive circuit – for an inductive circuit it makes sense that I have to provide additional VA to power the magnetic field but in this case the math makes more intuitive sense.



Thanks,


Brian

[mechminsk]

The intantaneous power is not time dependent. The proof is given in this video.

[mikefocal]

hi, great job, but i have a question : the power starts negative?

[gregorykotoch]

I can't believe that, as a non engineer, I understood this lecture.

[brainseva]

is there a video where you prove the "grand daddy power equation"? i'm struggling with a text book i have that does the proof of that.

[ahmadkhaliel]

thank you very much
I have a question
how the inductor deliver a power to the circuit from 0 to π /2 before it absorb from the circuit?