filmov
tv
Find a Splitting Field of x^3-1 over ℚ
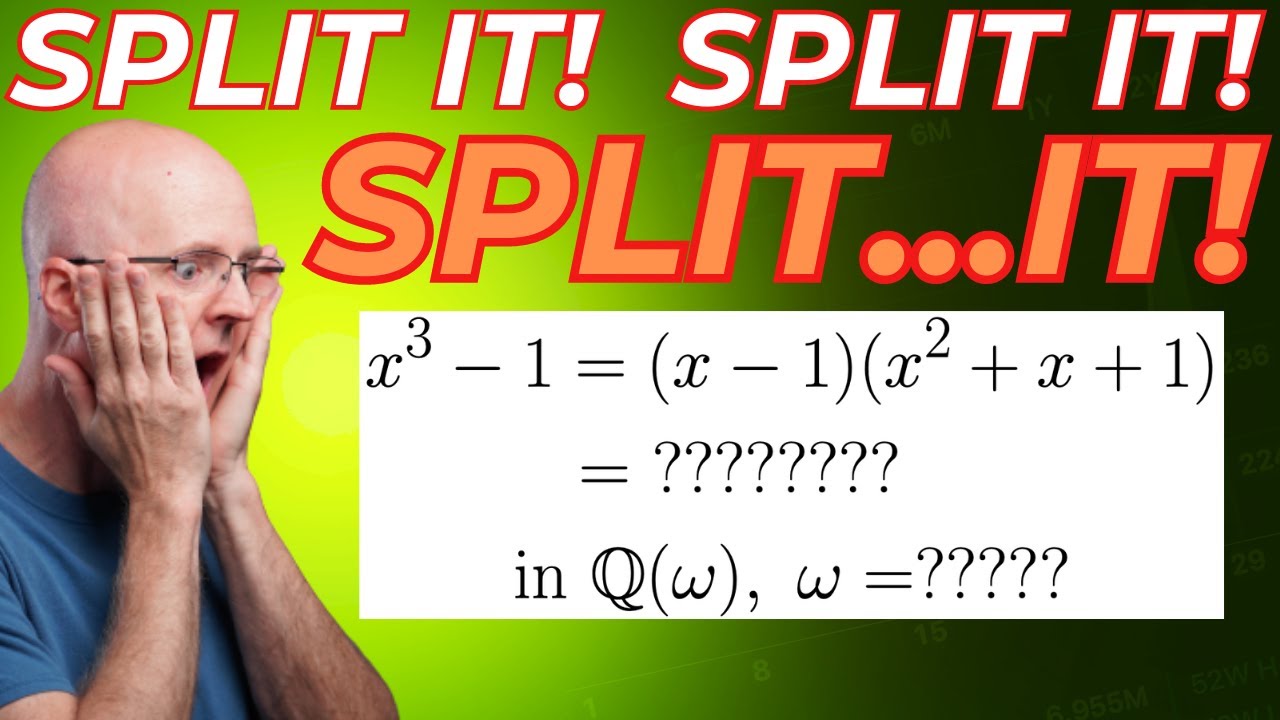
Показать описание
We find a splitting field for the polynomial f(x)=x^3-1 over the rationals ℚ. It is ℚ(ω), where ω = -1/2 + i*√3/2 = e^(i*2π/3) (and ω^2 = -1/2 - i*√3/2 = e^(i*4π/3)). This splitting field is a degree 2 extension of ℚ because the minimal polynomial of ω over ℚ is x^2 + x + 1, which has degree 2.
#AbstractAlgebra #FieldTheory #SplittingField
Links and resources
===============================
AMAZON ASSOCIATE
As an Amazon Associate I earn from qualifying purchases.
#AbstractAlgebra #FieldTheory #SplittingField
Links and resources
===============================
AMAZON ASSOCIATE
As an Amazon Associate I earn from qualifying purchases.
 0:04:02
0:04:02
 0:06:14
0:06:14
 0:15:16
0:15:16
 0:12:28
0:12:28
 0:06:15
0:06:15
 0:07:01
0:07:01
 0:06:38
0:06:38
 0:06:57
0:06:57
 0:07:01
0:07:01
 0:18:08
0:18:08
 0:04:37
0:04:37
 0:07:20
0:07:20
 0:10:50
0:10:50
 0:02:55
0:02:55
 0:02:05
0:02:05
 0:37:05
0:37:05
 0:23:40
0:23:40
 0:14:12
0:14:12
 0:17:27
0:17:27
 0:09:51
0:09:51
 0:06:43
0:06:43
 0:09:06
0:09:06
 0:13:05
0:13:05
 0:10:35
0:10:35