Generating a random nonconvex polygon

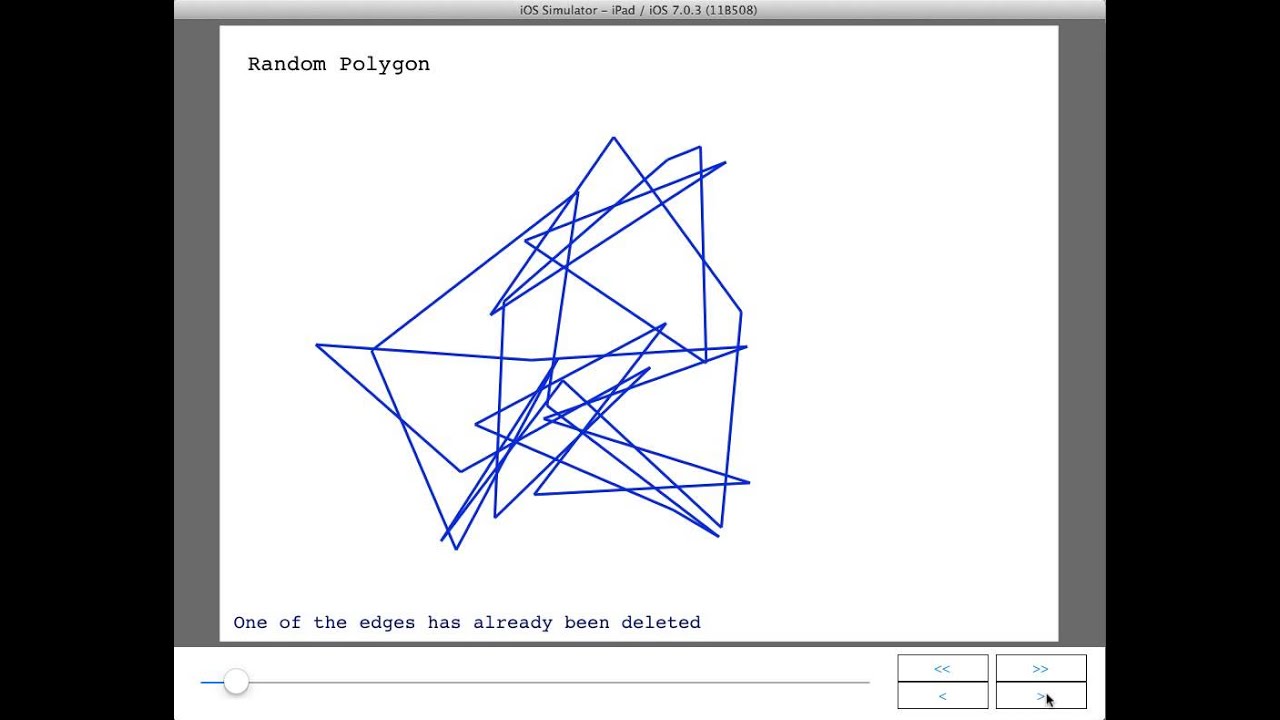
Uses a variant of the 2-opt moves heuristic to generate a random, nonconvex polygon.

Algorithm steps:

1) Generate a polygon of n random vertices lying within a bounding rectangle, by starting at an arbitrary point and performing a random walk. The step size is random but weighted towards steps that are smaller if n is large. This reduces the number of crossings in the initial polygon.

2) Perform a plane sweep, detecting points where polygon edges properly intersect ('cross'). If there are no crossing points, we are done.

3) Order these crossing points to process first the points that yield the greatest reduction in the polygon's boundary length when the 2-opt heuristic is applied.

4) For each ordered crossing point p, where edge a1a2 crosses edge b1b2:

a) If either of the two edges crossing at p have been deleted, skip.
b) Remove a1a2 and b1b2.
c) Reverse the order of either a2..b1 or b2..a1, whichever of these sequences is shorter (we can make this decision in O(1) time if the vertices are numbered; the reversal then takes time linear in the length of the sequence).
d) Add edges a1b1 and a2b2

5) Repeat from step 2.

This algorithm improves on the O(n^4) running time by processing a number of crossing points after each sweep operation. Its total running time is probably between O(n^2 log n) and O(n^3), depending upon how 'tangled' the initial polygon is.

References:

2) 2-opt heuristic: