filmov
tv
Motivating Eigenvalues and Eigenvectors with Differential Equations

Показать описание
This video *derives* the eigenvalues and eigenvectors of a matrix "A" to solve the matrix system of equations dx/dt = A*x.
@eigensteve on Twitter
This video was produced at the University of Washington
%%% CHAPTERS %%%
0:00 Overview
1:26 Problem Setup
2:33 The Simplest System of ODEs: Decoupled (Diagonal) Dynamics
10:25 Finding a Coordinate System Where Dynamics Look Diagonal
15:42 Deriving the Eigenvalue/Eigenvector Equation
19:03 A Picture of the Eigenvalue Equation
22:27 Recap and Summary
@eigensteve on Twitter
This video was produced at the University of Washington
%%% CHAPTERS %%%
0:00 Overview
1:26 Problem Setup
2:33 The Simplest System of ODEs: Decoupled (Diagonal) Dynamics
10:25 Finding a Coordinate System Where Dynamics Look Diagonal
15:42 Deriving the Eigenvalue/Eigenvector Equation
19:03 A Picture of the Eigenvalue Equation
22:27 Recap and Summary
Motivating Eigenvalues and Eigenvectors with Differential Equations
Eigenvectors and eigenvalues | Chapter 14, Essence of linear algebra
Eigenvalues and Eigenvectors: Part 1/4 'Motivation'
Lecture 6 (Part 4): Motivation & introduction for eigenvalues and eigenvectors; visualizations
Eigen values and Eigen vectors in 3 mins | Explained with an interesting analogy
Motivation for Eigenvectors
Eigenvectors and Eigenvalues | Motivation for their definitions
7.3.4-ODEs: Eigenvalue Problem Motivation
Motivation on Eigenvalues and Eigenvectors
Harvard AM205 video 5.1 - Introduction to eigenvalue problems
The RIGHT way to think about matrices, eigenvalues and eigenvectors
Eigenvalues & Eigenvectors : Data Science Basics
Eigenvalues and Eigenvectors
Real life example of Eigen values and Eigen vectors
Eigenvalues and Eigenvectors
Different Cases Of Eigen Values #maths #eigenvalue #eigenvalues #viral #mathstrending
Eigenvalues and Eigenvectors use in daily life.
Definition and Examples of EIGENVALUES and EIGENVECTORS | FREE Linear Algebra Course
Machine Learning Maths | EigenValues And EigenVectors | Part 5 | Eduonix
Harvard AM205 video 5.6 - QR algorithm
Why greatest Mathematicians are not trying to prove Riemann Hypothesis? || #short #terencetao #maths
Using determinants to compute eigenvalues & eigenvectors
15 - What are Eigenvalues and Eigenvectors? Learn how to find Eigenvalues.
Eigenvalue Problems: 1 Motivation
Комментарии
 0:23:58
0:23:58
 0:17:16
0:17:16
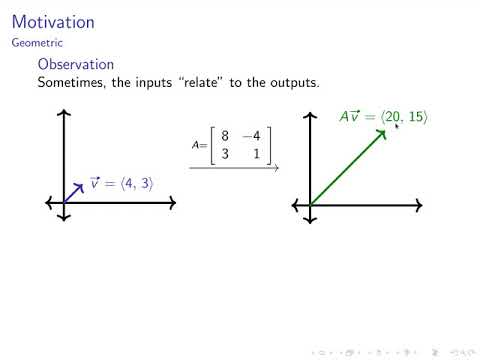 0:07:04
0:07:04
 0:27:06
0:27:06
 0:02:55
0:02:55
 0:07:58
0:07:58
 0:10:41
0:10:41
 0:04:14
0:04:14
 0:30:11
0:30:11
 0:29:06
0:29:06
 0:14:33
0:14:33
 0:11:58
0:11:58
 0:33:57
0:33:57
 0:04:44
0:04:44
 0:14:15
0:14:15
 0:00:22
0:00:22
 0:00:52
0:00:52
 0:05:28
0:05:28
 0:12:16
0:12:16
 0:24:00
0:24:00
 0:00:38
0:00:38
 0:04:36
0:04:36
 0:13:08
0:13:08
 0:07:32
0:07:32