filmov
tv
Lagrange Error Bound to Find Error when using Taylor Polynomials

Показать описание
The theorem all looks a bit complicated but really it just boils down to taking some derivatives and then trying to maximize that function over a given interval. The rest of it is 'plug and chug'!
Lagrange Error Bound to Find Error when using Taylor Polynomials
Lagrange Error Bound
Calculus BC – 10.12 Lagrange Error Bound
Worked example: estimating sin(0.4) using Lagrange error bound | AP Calculus BC | Khan Academy
Taylor's Remainder Theorem
Lagrange Remainder (Error Bound)
A Swift Introduction to Lagrange Error Bounds (Taylor Series) | #some3
(Lagrange Error Bound) A first Example!
Lagrange Error Bound 1
Lagrange Error Bound
Review of Lagrange Error Bound and Alternating Series Error for the BC Calculus Exam
Lagrange error bound formula
Error Bounds for Taylor Polynomial Approximations
Worked example: estimating e_ using Lagrange error bound | AP Calculus BC | Khan Academy
Proof of Lagrange Error Bound
Lagrange Error Bound
Lagrange Polynomial Interpolation Error Bound Example
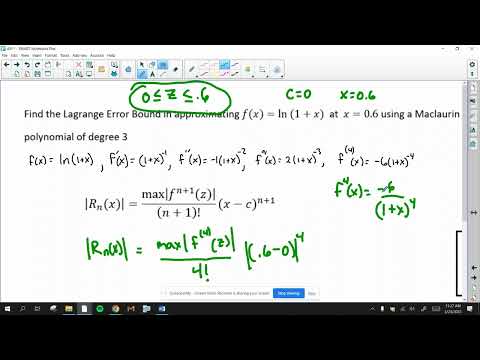
Remainder Estimation Theorem (Lagrange Error Bound) Example #1
Lagrange Error Bound pg 8, pt 1
Lagrange Error Bound Part 1
Lagrange Error Bound
Lagrange Error Bound (Again) pg 4
Calculus BC – 10.10 Alternating Series Error Bound
Lagrange Error Bound
Комментарии
 0:15:14
0:15:14
 0:04:56
0:04:56
 0:19:21
0:19:21
 0:08:46
0:08:46
 0:14:08
0:14:08
 0:13:29
0:13:29
 0:08:37
0:08:37
 0:08:29
0:08:29
 0:14:20
0:14:20
 0:10:26
0:10:26
 0:15:10
0:15:10
 0:02:43
0:02:43
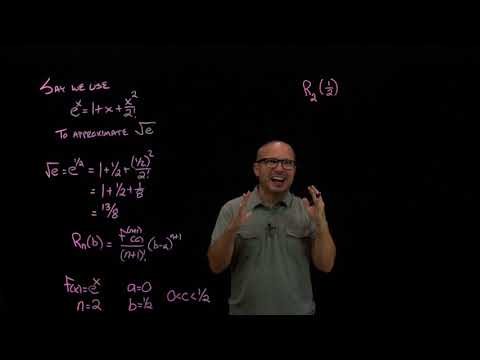 0:11:41
0:11:41
 0:09:19
0:09:19
 0:09:22
0:09:22
 0:20:46
0:20:46
 1:15:05
1:15:05
 0:02:41
0:02:41
 0:07:38
0:07:38
 0:09:20
0:09:20
 0:06:36
0:06:36
 0:13:28
0:13:28
 0:21:17
0:21:17
 0:05:39
0:05:39