filmov
tv
Solve linear equations (a-b)x+(a+b)y=a^2-2ab-b^2; (a+b)(x+y)=a^2+b^2 || Cross Multiplication Method

Показать описание
Question:
Solve the following pair of linear equations:
(a-b)x+(a+b)y=a^2-2ab-b^2; (a+b)(x+y)=a^2+b^2
Videos from Chapter 3 (Pair of linear equation in two variables)
Example 19: A boat goes 30 km upstream and 44 km downstream in10 hours. In 13 hours, it can go 40 km upstream and 55 km down-stream. Determine the speed of the stream and that of the boat in still water.
HOTS:
Solve for x and y:
37x + 41y = 70 ; 41x + 37y = 86.
Ex. 3.6 Q. 1(i)
Solve the pair of equations by reducing them to a pair of linear equations
1/2x+1/3y= 2 ; 1/3x+1/2y=13/6
Ex. 3.6 Q. 1(ii)
Solve the pair of equations by reducing them to a pair of linear equations
2/√x+3/√y=2; 4/√x-9/√y=-1
Ex. 3.6 Q1(iv)
Solve the pair of equations by reducing them to a pair of linear equations
5/(x-1)+1/(y-2)=2; 6/(x-1)-3/(y-2)=1
Ex. 3.6 Q.1(vii)
Solve the pair of equations by reducing them to a pair of linear equations
10/(x+y)+2/(x-y)=4; 15/(x+y)-5/(x-y)=-2
Ex. 3.6 Q. 1(viii)
Solve the pair of equations by reducing them to a pair of linear equations
1/(3x+y)+1/(3x-y)=3/4; 1/2(3x+y) -1/2(3x-y) =-1/8
Ex. 3.7 (optional) Q. 1
The ages of two friends Ani and Biju differ by 3 years. Ani’s father Dharam is twice as old as Ani and Biju is twice as old as his sister Cathy. The ages of Cathy and Dharam differ by 30 years. Find the ages of Ani and Biju.
Ex. 3.7 (optional) Q. 2
One says, “Give me a hundred, friend! I shall then become twice as rich as you”. The other replies, “If you give me ten, I shall be six times as rich as you”. Tell me what is the amount of their (respective) capital?
Ex. 3.7 (optional) Q. 3
A train covered a certain distance at a uniform speed. If the train would have been10 km/h faster, it would have taken 2 hours less than the scheduled time. And, if the train were slower by 10 km/h; it would have taken 3 hours more than the scheduled time. Find the distance covered by the train.
Ex. 3.7 (optional) Q. 4
The students of a class are made to stand in rows. If 3 students are extra in a row, there would be 1 row less. If 3 students are less in a row, there would be 2 rows more. Find the number of students in the class.
Ex. 3.7 (Optional) Q. 5
In a ∆ABC, ∠C = 3∠B = 2 (∠A +∠B). Find the three angles.
Ex. 3.7 (Optional) Q. 6
Draw the graphs of the equations 5x – y = 5 and 3x – y = 3. Determine the co-ordinates of the vertices of the triangle formed by these lines and the y axis.
Ex. 3.7 (Optional) Q. 7(i)
Solve the following pair of linear equations:
px + qy = p – q ; qx – py = p + q
Ex. 3.7 (Optional) Q. 7(ii)
Solve the following pair of linear equations:
ax + by = c ; bx+ay =1+c
Ex. 3.7 (Optional) Q. 7(iii)
Solve the following pair of linear equations:
x/a-y/b=0; ax+by=a^2+b^2
Like our facebook page:
follow us at twitter:
follow us at google plus:
follow us at instagram:
Solve the following pair of linear equations:
(a-b)x+(a+b)y=a^2-2ab-b^2; (a+b)(x+y)=a^2+b^2
Videos from Chapter 3 (Pair of linear equation in two variables)
Example 19: A boat goes 30 km upstream and 44 km downstream in10 hours. In 13 hours, it can go 40 km upstream and 55 km down-stream. Determine the speed of the stream and that of the boat in still water.
HOTS:
Solve for x and y:
37x + 41y = 70 ; 41x + 37y = 86.
Ex. 3.6 Q. 1(i)
Solve the pair of equations by reducing them to a pair of linear equations
1/2x+1/3y= 2 ; 1/3x+1/2y=13/6
Ex. 3.6 Q. 1(ii)
Solve the pair of equations by reducing them to a pair of linear equations
2/√x+3/√y=2; 4/√x-9/√y=-1
Ex. 3.6 Q1(iv)
Solve the pair of equations by reducing them to a pair of linear equations
5/(x-1)+1/(y-2)=2; 6/(x-1)-3/(y-2)=1
Ex. 3.6 Q.1(vii)
Solve the pair of equations by reducing them to a pair of linear equations
10/(x+y)+2/(x-y)=4; 15/(x+y)-5/(x-y)=-2
Ex. 3.6 Q. 1(viii)
Solve the pair of equations by reducing them to a pair of linear equations
1/(3x+y)+1/(3x-y)=3/4; 1/2(3x+y) -1/2(3x-y) =-1/8
Ex. 3.7 (optional) Q. 1
The ages of two friends Ani and Biju differ by 3 years. Ani’s father Dharam is twice as old as Ani and Biju is twice as old as his sister Cathy. The ages of Cathy and Dharam differ by 30 years. Find the ages of Ani and Biju.
Ex. 3.7 (optional) Q. 2
One says, “Give me a hundred, friend! I shall then become twice as rich as you”. The other replies, “If you give me ten, I shall be six times as rich as you”. Tell me what is the amount of their (respective) capital?
Ex. 3.7 (optional) Q. 3
A train covered a certain distance at a uniform speed. If the train would have been10 km/h faster, it would have taken 2 hours less than the scheduled time. And, if the train were slower by 10 km/h; it would have taken 3 hours more than the scheduled time. Find the distance covered by the train.
Ex. 3.7 (optional) Q. 4
The students of a class are made to stand in rows. If 3 students are extra in a row, there would be 1 row less. If 3 students are less in a row, there would be 2 rows more. Find the number of students in the class.
Ex. 3.7 (Optional) Q. 5
In a ∆ABC, ∠C = 3∠B = 2 (∠A +∠B). Find the three angles.
Ex. 3.7 (Optional) Q. 6
Draw the graphs of the equations 5x – y = 5 and 3x – y = 3. Determine the co-ordinates of the vertices of the triangle formed by these lines and the y axis.
Ex. 3.7 (Optional) Q. 7(i)
Solve the following pair of linear equations:
px + qy = p – q ; qx – py = p + q
Ex. 3.7 (Optional) Q. 7(ii)
Solve the following pair of linear equations:
ax + by = c ; bx+ay =1+c
Ex. 3.7 (Optional) Q. 7(iii)
Solve the following pair of linear equations:
x/a-y/b=0; ax+by=a^2+b^2
Like our facebook page:
follow us at twitter:
follow us at google plus:
follow us at instagram:
Комментарии
 0:06:02
0:06:02
 0:12:15
0:12:15
 0:06:42
0:06:42
 0:04:27
0:04:27
 0:06:53
0:06:53
 0:08:01
0:08:01
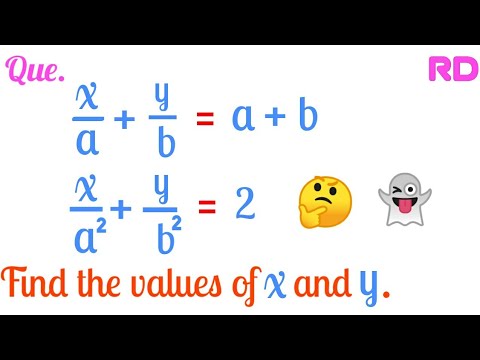 0:03:54
0:03:54
 0:33:03
0:33:03
 0:02:30
0:02:30
 0:05:09
0:05:09
 0:01:56
0:01:56
 0:04:21
0:04:21
 0:03:20
0:03:20
 0:05:02
0:05:02
 0:08:28
0:08:28
 0:03:29
0:03:29
 0:06:53
0:06:53
 0:03:47
0:03:47
 0:07:01
0:07:01
 0:08:08
0:08:08
 0:02:30
0:02:30
 0:04:08
0:04:08
 0:03:46
0:03:46
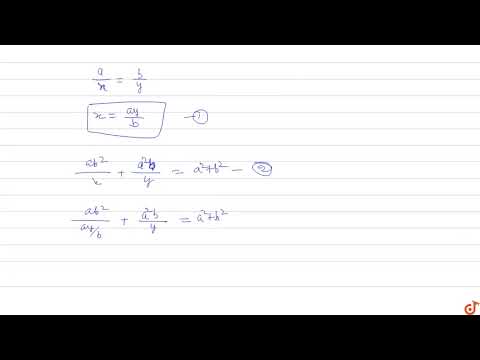 0:03:05
0:03:05