filmov
tv
Plotting a sine rose curve by rotation of a cosine rose curve and animation of rotating polar curve.
Показать описание
Questions or requests? Post your comments below, and I will respond within 24 hours.
Plotting a sine rose curve by rotation of a cosine rose curve and animation of rotating polar curve.
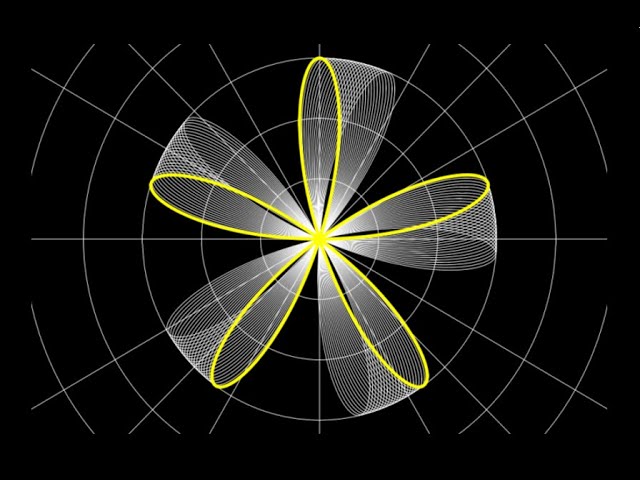
In this video, we are given the polar equation of a rose curve r=3cos(5*theta). Because the coefficient of theta is odd, the rose has the same number of petals as the coefficient. We are asked to use the graph of the original rose curve to sketch the graph of r=3sin(5*theta).
To get this done, we use the trig identity sin(theta)=cos(theta-pi/2). In other words, we obtain the sine by advancing the cosine through an angle of pi/2. We apply the identity to our cosine rose, then factor out the 5 to obtain r=3cos(5(theta-pi/10)). This is a rotation of the polar curve counterclockwise through an angle of pi/10.
Finally, we use a computer algebra system to animate the rotation of the rose curve, and we obtain our picture of r=3sin(5*theta). So we successfully plot a sine rose curve using a rotation. We dramatically fade out leaving the graph of r=3sin(5*theta) in the foreground (yay, new skill!).
Plotting a sine rose curve by rotation of a cosine rose curve and animation of rotating polar curve.
In this video, we are given the polar equation of a rose curve r=3cos(5*theta). Because the coefficient of theta is odd, the rose has the same number of petals as the coefficient. We are asked to use the graph of the original rose curve to sketch the graph of r=3sin(5*theta).
To get this done, we use the trig identity sin(theta)=cos(theta-pi/2). In other words, we obtain the sine by advancing the cosine through an angle of pi/2. We apply the identity to our cosine rose, then factor out the 5 to obtain r=3cos(5(theta-pi/10)). This is a rotation of the polar curve counterclockwise through an angle of pi/10.
Finally, we use a computer algebra system to animate the rotation of the rose curve, and we obtain our picture of r=3sin(5*theta). So we successfully plot a sine rose curve using a rotation. We dramatically fade out leaving the graph of r=3sin(5*theta) in the foreground (yay, new skill!).
0:05:07
PreCalculus - Polar Coordinates (16 of 35) Graphing Polar Equations: r=3sin3(theta), Roses
0:01:56
Plotting a sine rose curve by rotation of a cosine rose curve and animation of rotating polar curve.
0:12:12
PreCalculus - Polar Coordinates (14 of 35) Graphing Polar Equations: r=3cos4(theta), Roses
0:08:17
PreCalculus - Polar Coordinates (15 of 35) Graphing Polar Equations: r=3cos3(theta), Roses
0:00:13
A short survey of polar sine roses, animations of rose curves using linear interpolation. #shorts
0:03:26
How to Graph Any Polar Curves: Cardioid Example r = 1 + cos(theta)
0:04:54
Sketch the Polar Graph of r = a sin(nθ) Example (Rose Curve)
0:11:22
Graphing a Polar Curve r=sin(2theta)
0:10:58
graph rose curves, Sin, n is even
0:00:47
Polar Graph of r = 2 sin (4 theta)
0:10:46
Polar Coordinates and Graphing Polar Equations
0:09:11
Polar coordinates Graph folium r equal sin 3 theta
0:00:48
Polar Graph of r = 2 sin (5 theta)
0:02:45
Find area of shaded region of polar curve graph r = sin 2 theta. Rose with four petals
0:08:12
Identify and graph polar equation r = 4 sin (5 theta). Rose with five petals. Test for Symmetry
0:01:29
Polar Coordinates | flower 🌸🌼🌻| r=Sin(t)
0:00:48
Polar Graph of r = 2 sin (2 theta)
0:33:50
Finding Area In Polar Coordinates
0:07:01
Identify and graph polar equation r = 2 sin (3 theta). Rose with three petals. Test for Symmetry
0:12:16
HPC 10.8.2, Intro to rose curves, especially sine
0:00:48
Polar Graph of r = 2 sin (3 theta)
0:15:37
Polar Curve: r=sin(Θ)
0:00:48
Polar Graph of r = 2 sin (9 theta)
0:10:32
graph rose curves with Sin, n is odd
Комментарии