filmov
tv
The sum ∑_(r=2)^∞▒1/(r²-1) is equal to:a)1 b)3/4 c)4/3 d)None of these

Показать описание
Find the value of the expression ∑_(i=1)^n▒∑_(j=1)^i▒∑_(k=1)^j▒1
Sequence and series class 11 JEE
The different numbers occurring in any particular sequence are known as its terms. The terms of a sequence are denoted by
a1, a2, a3,….,an
If a sequence has a finite number of terms then it’s known as a finite sequence. A sequence is termed as infinite if it is not having a definite number of terms. The nth term of an AP is given by
a + (n-1) d.
Between any two numbers ‘a’ and ‘b’, n numbers can be inserted such that the resulting sequence is an Arithmetic Progression. A1 , A2 , A3,……,An be n numbers between a and b such that a, A1 , A2 , A3,……,An, b is in A.P.
Here, a is the 1st term and b is (n+2)th term. Therefore,
b = a + d[(n + 2) – 1] = a + d (n + 1).
Hence, common difference (d) = (b-a)/(n+1)
Now, A1= a+d= a+((b-a)/(n+1)),
A2= a+2d = a+ ((2(b-a)/(n+1)),
An =a+nd= a+ ((n(b-a)/(n+1))}
The nth term of a geometric progression is given by an = arn-1
Sequence and Series Formulas
List of some basic formula of arithmetic progression and geometric progression are,
Arithmetic Progression Geometric Progression
Sequence a, a+d, a+2d,……,a+(n-1)d,…. a, ar, ar2,….,ar(n-1),…
Common Ratio Successive term – Preceding term
Common difference = d = a2 – a1
Successive term/Preceding term
Common ratio = r = ar(n-1)/ar(n-2)
General Term (nth Term) an = a + (n-1)d an = ar(n-1)
nth term from the last term an = l – (n-1)d an = 1/r(n-1)
Sum of first n terms sn = n/2(2a + (n-1)d) sn = a(rn)/(1-r) if r 1
sn = a(rn -1)/(r – 1)………(2) if r greater than 1
Sequence and Series Examples
Question 1: If 4,7,10,13,16,19,22……is a sequence, Find:
Common difference
nth term
21st term
Solution: Given sequence is, 4,7,10,13,16,19,22……
a) The common difference = 7 – 4 = 3
b) The nth term of the arithmetic sequence is denoted by the term Tn and is given by Tn = a + (n-1)d, where “a” is the first term and d, is the
common difference.
Tn = 4 + (n – 1)3 = 4 + 3n – 3 = 3n + 1
c) 21st term as: T21 = 4 + (21-1)3 = 4+60 = 64.
Question 2: Consider the sequence 1,4,16,64,256,1024….. Find the common ratio and 9th term.
Solution: The common ratio (r) = 4/1 = 4
The preceding term is multiplied by 4 to obtain the next term.
The nth term of the geometric sequence is denoted by the term Tn and is given by Tn = ar(n-1)
where a is the first term and r is the common ratio.
Here a = 1, r = 4 and n = 9
So, 9th term is can be calculated as T9 = 1* (4)(9-1)= 48 = 65536.
Sequences and Series Class 11
sequence and series class 11 revision,sequence and series class 11th,sequence and series class 11 jee,sequence and series class 11 all formula,sequence and series class 11 basics,sequence and series class 11 cbse,sequence and series class 11 full explanation,sequence and series class 11 examfear,sequence and series class 11 iit jee,sequence and series class 11 jee mains,sequence and series class 11 jee mains questions,sequence and series class 11 jee advanced
Комментарии
 0:03:21
0:03:21
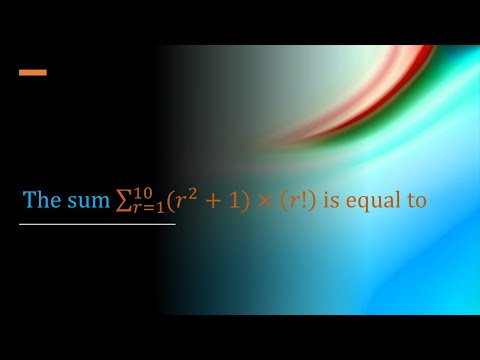 0:01:59
0:01:59
 0:03:21
0:03:21
 0:08:16
0:08:16
 0:04:22
0:04:22
 0:06:29
0:06:29
 0:09:19
0:09:19
 0:00:50
0:00:50
 1:55:56
1:55:56
 0:07:06
0:07:06
 0:03:57
0:03:57
 0:03:20
0:03:20
 0:01:40
0:01:40
 0:10:10
0:10:10
 0:10:04
0:10:04
 0:07:13
0:07:13
 0:07:40
0:07:40
 0:00:32
0:00:32
 0:01:28
0:01:28
 0:08:58
0:08:58
 0:00:16
0:00:16
 0:00:11
0:00:11
 0:04:09
0:04:09
 0:00:56
0:00:56