filmov
tv
Proof: How to Prove the Sum of Two Cubes a^3 + b^3 = (a+b)(a^2-ab+b^2)
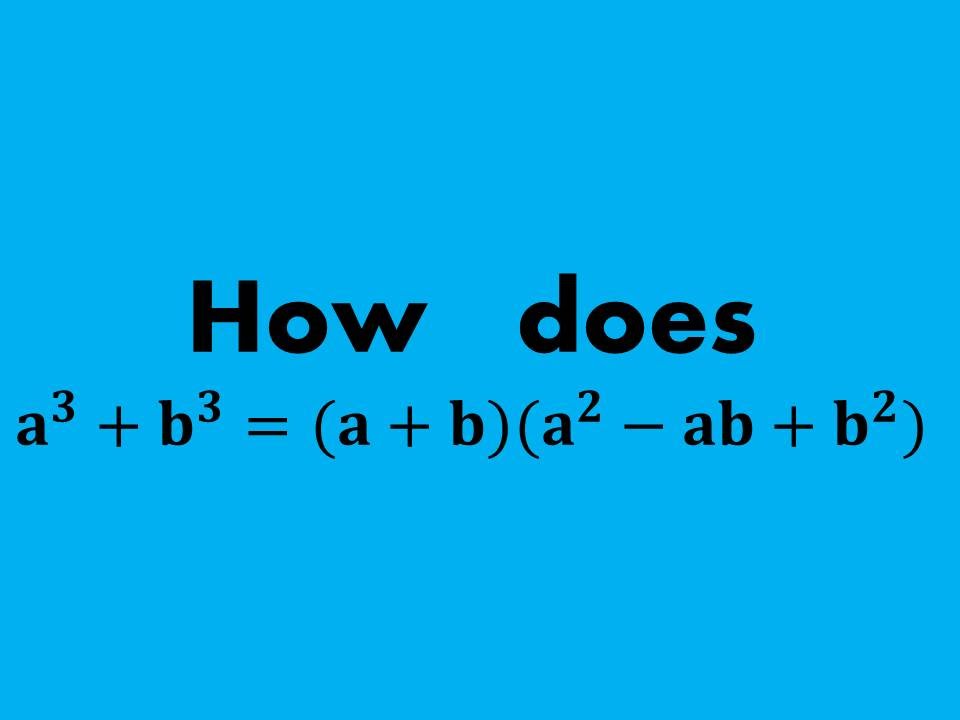
Показать описание
Don't forget to like, comment, and subscribe!!!
The problem: How/Why does a^3 + b^3 = (a+b)(a^2-ab+b^2)
The solution: by simply adding zero twice and then finding two terms that add to zero, we can complete the proof.
The problem: How/Why does a^3 + b^3 = (a+b)(a^2-ab+b^2)
The solution: by simply adding zero twice and then finding two terms that add to zero, we can complete the proof.
What's the difference between 'proof' and 'prove'?
How many ways are there to prove the Pythagorean theorem? - Betty Fei
9 tips to help you PROVE MATH THEOREMS
Only U.S. President to prove a theorem
Direct Proof: Prove that if 5x - 7 is odd, then 9x + 2 is even
Can you prove it?? #shorts #shortsvideo #explore #youtubeshorts #aptitude #proof #provethat
How to Prove that Muhammad was REALLY a Prophet
Easy Test to Prove Earth is Flat #science
PROOF That Loyalty Can Conquer ANY Obstacle!
How to prove the Pythagoras Theorem in 4 steps | asH math
When to use proof, prove, belief, and believe
How to Prove Math Theorems | 1st Ex: Even + Odd = Odd
How to Mathematically Prove Jesus's Resurrection
Atheist professor tries to prove that God doesn’t exist- Part 1
How to prove any number irrational #shorts #mathshustle
Prove Tan-Chord Theorem Grade 12 Mathematics November 2021 (Circle Theorems)
3 Facts that PROVE the Resurrection of Jesus - Simple Explanation #Shorts
Evidence of God in Math?
Prove that 2=3 || How To Proof 2=3
Why greatest Mathematicians are not trying to prove Riemann Hypothesis? || #short #terencetao #maths
Use a Two Column Proof to Prove Congruence Using CPCTC - Congruent Triangles
How To Prove the Angle At Centre Theorem | Trick | Grade 11&12 Euclidean Geometry | with MrSir M...
How to Prove the Bible is True
Prove that root 2 Is a rational number #solutions #realnumbers
Комментарии
 0:04:22
0:04:22
 0:05:17
0:05:17
 0:15:07
0:15:07
 0:01:00
0:01:00
 0:03:54
0:03:54
 0:00:19
0:00:19
 0:26:22
0:26:22
 0:00:50
0:00:50
 0:00:40
0:00:40
 0:00:40
0:00:40
 0:03:43
0:03:43
 0:08:35
0:08:35
 0:00:42
0:00:42
 0:00:47
0:00:47
 0:00:16
0:00:16
 0:05:31
0:05:31
 0:01:00
0:01:00
 0:00:54
0:00:54
 0:02:47
0:02:47
 0:00:38
0:00:38
 0:06:02
0:06:02
 0:12:00
0:12:00
 0:04:08
0:04:08
 0:00:16
0:00:16