filmov
tv
More advanced ratio problem--with Algebra (HD version)

Показать описание
More advance ratio problem with algebra.
More advanced ratio problem--with Algebra (HD version)
Algebra: Advanced Ratio Problems
842 More advanced ratio problem with Algebra
022 More advanced ratio problem with Algebra HD version
Ratio Word Problems - Algebra 1
Algebra - 22 More advanced ratio problem--with Algebra (HD version)
Algebra - 22 More advanced ratio problem--with Algebra (HD version)
27 More advanced ratio problem with Algebra HD version
More advanced ratio problem--with Algebra (HD version) (Bangla)
More advanced ratio problem with Algebra HD version (Bangla)
Algebraic Ratios
Ratio and Proportion Word Problems - Math
Working With Ratios | Algebra
Ratio problem with basic algebra | Linear equations and inequalities | Algebra Basics | Khan Academy
More advanced ratio problem with Algebra HD version Bangla
Art of Problem Solving: Introducing Ratios
Algebra 1/2 Lesson 100 Advanced Ratio Problems
Solving Algebraic Fractions | Equivalent Ratios using Algebra | Grade 7-9 Series | GCSE Maths Tutor
Time and Work Problems - Shortcuts and Tricks
How to solve word problems using models and algebra - Singapore Math - Ratio
Algebra: Ratio Problems
Ratios | All About Ratios
The 5 Hardest Vector Questions on the Maths GCSE (Including Ratios) | Grade 9+ | GCSE Maths Tutor
Memorization Trick for Graphing Functions Part 1 | Algebra Math Hack #shorts #math #school
Комментарии
 0:09:58
0:09:58
 0:03:34
0:03:34
 0:09:24
0:09:24
 0:09:58
0:09:58
 0:06:55
0:06:55
 0:09:58
0:09:58
 0:09:58
0:09:58
 0:09:58
0:09:58
 0:05:36
0:05:36
 0:10:09
0:10:09
 0:01:43
0:01:43
 0:13:27
0:13:27
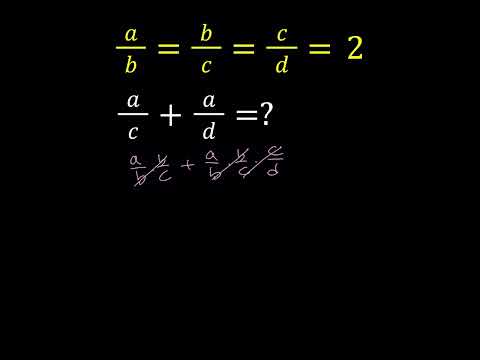 0:00:32
0:00:32
 0:05:12
0:05:12
 0:10:09
0:10:09
 0:05:56
0:05:56
 0:09:49
0:09:49
 0:26:38
0:26:38
 0:33:55
0:33:55
 0:10:47
0:10:47
 0:02:59
0:02:59
 0:05:57
0:05:57
 0:42:38
0:42:38
 0:00:15
0:00:15