Proof of the Sum-Difference Formulas - Part 1

In this video, I demonstrate how to prove the following sum-difference formulas, or trigonometric identities:

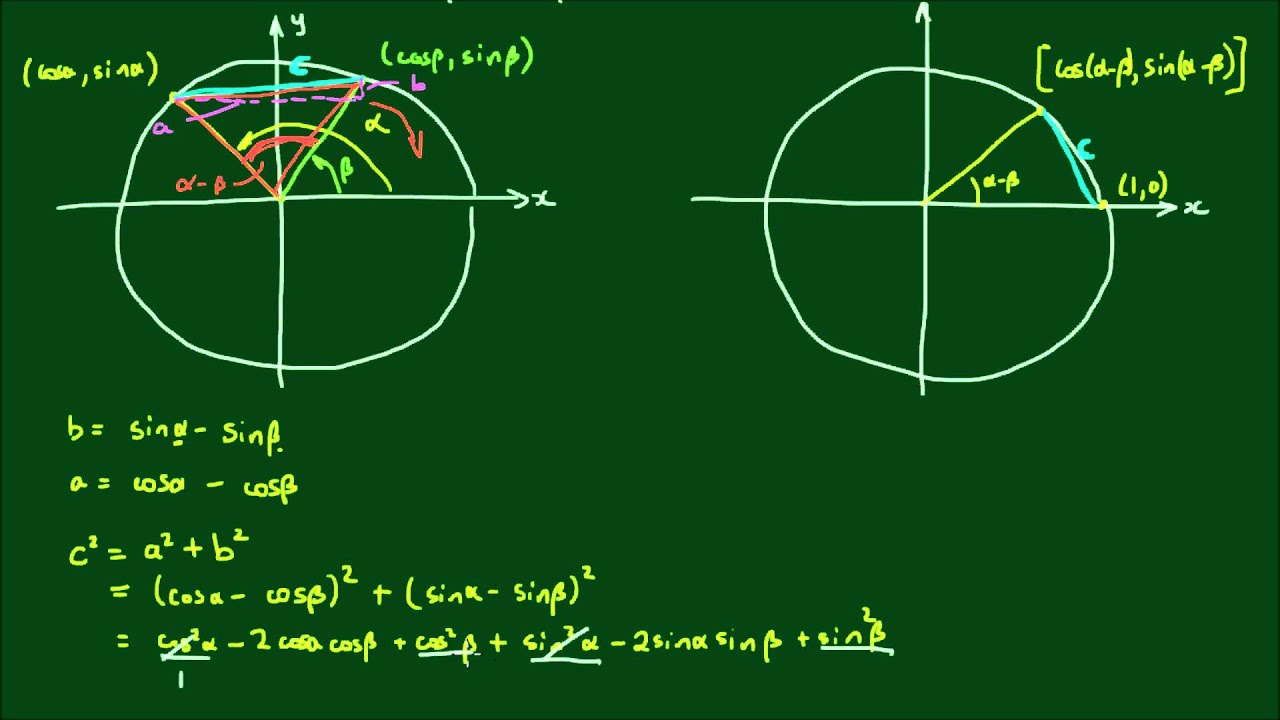
cos(a - b) = cos(a)*cos(b) + sin(a)*sin(b)
cos(a + b) = cos(a)*cos(b) - sin(a)*sin(b)
sin(a + b) = sin(a)*cos(b) + sin(b)*cos(a)
sin(a - b) = sin(a)*cos(b) - sin(b)*cos(a)

From the results above, I also derive the following identities:

cos(2a) = cos^2(a) - sin^2(a)
sin(2a) = 2*sin(a)*cos(a)

Thanks for watching. Please give me a "thumbs up" if you have found this video helpful.

Please ask me a maths question by commenting below and I will try to help you in future videos.

cos(x - y) = cos(x)*cos(y) + sin(x)*sin(y)
cos(x + y) = cos(x)*cos(y) - sin(x)*sin(y)
sin(x + y) = sin(x)*cos(y) + sin(x)*cos(y)
sin(x - y) = sin(x)*cos(y) - sin(x)*cos(y)
cos(2x) = cos^2(x) - sin^2(x)
sin(2x) = 2*sin(x)*cos(x)

[stephencollins]

Thank you! This was very helpful seeing how it these identities are derived. This is so much better than memorizing stuff that doesn't make sense.

[hongningsuen]

I would like to introduce to you a really general but very simple proof for all compound angle formulae with any positive angles a and b, which can be a > b or a < b. The starting formula should be cos (a - b). The unit circle is divided into 2 sectors by the two unit vectors having angles a and b. The length of the chord of the minor sector can be found by distance formula when the coordinates of the unit vectors are derived as x = cos a or b, and y = sin a or b. The reason for choosing cos (a - b) is that the angle between the unit radii forming one of the two sectors of unit circle is (a - b) when a > b, and - (a - b) when a < b, whatever the values of a and b. By rotational transformation about origin, the sector with this angle moves to a new position with original unit radius for angle a lying on the x-axis. The original unit radius for angle b will move to have a new angle = (a - b) or - (a - b). Hence a new set of coordinates for ends of the rotated chord can be established. A second distance equation for the chord length equal to that from the first distance equation can be established. With algebraic manipulation, the formula for cos (a - b) can be proved in the most general way. With this formula proven, other compound angle formulae can be derived by substituting (-b) for b, (90 + a) for a into the proven formula and substituting sin/cos for tan. I would like to call this method equal chords of rotated sectors method.

[rayxr]

I think there's a problem at 8:57: Shouldn't *a2= 1 - cos(alpha-beta)?*

Let's consider the distance between the origin and the start of _a1_ on graph 2 to be _x._ That means the total horizontal distance of the triangle in graph 2 is _x + a1._ We know the total horizontal distance is equal to one, so we can use the equation _x + a1 = 1_ to solve for _a1._

Using the Pythagorean Theorem, we know _x = cos(alpha-beta)._ Therefore, the total horizontal distance of graph 2 is _cos(alpha-beta) + a1 = 1._ So if we subtract _cos(alpha-beta)_ on both sides we get *a1 = 1 - cos(alpha-beta).*

Does not matter once you square it, but it's still an error in a proof nonetheless. Great demonstration otherwise.

[vladimirmoravek]

[11:00/17:24] There is a simple DERIVATION of sin (a+/-b) and cos (+/-b) directly from the unit circle, and the DEFINITION of sin and cos functions. Try it!!

[jdlopez]

at min 12:55 you simply swapped gammas for Betas? That must be a mistake. So, right before you swapped them, your formula was:

cos(alpha + gamma) = cos (alpha) * cos(gamma) - sin (alpha) * sin (gamma) -- > I can agree with this formula; everything made sense 'til this point... but then you simply proceeded to swapping positive gamma for positive Beta ??

This is my point, if you were swapping gamma for beta again, you should be left with:

cos (alpha - Beta) = cos(alpha) * cos(Beta) - sin(alpha) * sin(-Beta)
or same as
cos (alpha - Beta) = cos(alpha) * cos(Beta) + sin(alpha) * sin(Beta) -- > which is the original formula.

would you please explain why did you just swapped Beta for Gamma, when you clearly stated that B = -1* Gamma

[zhuziyuan]

great explanation! i enjoy it alot ! cheers mate

[jdlopez]

In min 14:38 you mentioned that a phase shift of 90 degrees converts a cosine to a sine, that is true if both angles are positive angles. That is not the case for cos(17) and sine(-73); their results share opposing signs.

[coleabrahams]

2:22 Shouldn't the coordinate be (-cos alpha, sin alpha)?

[elizabethhenzell]

Hello. I am not a maths student, but someone who has a keen interest in the subject. it is decades since I did my maths exams! just to ask - is the Cosine / Sine point on the unit circle arrived at by where the radius touches the circle? Also, for Cos A Sine A I have seen on other maths sites that this is a negative quadrant for Cosine and positive for Sine. As we square the Cosine in the distance / Pythagoras formula I am guessing that we still get a positive for the Cosine and the Sine is still deducted a it is a positive being subtracted. Any help would be greatly accepted

[RahulKumar-scer]

How you take a-b angle in another circle???

[emmanuelalbazi]

Please can you solve the integral of cos(a/x)

[keyser]

DO WE HAVE ANY ALTERNATIVE METHODS???? LET ME KNOW IF THERE'S

[micahwright]

I thought Pythagoras Theorem only applies to right triangles?

[조민석-xo]

It is so difficult to see the diagram, nearly impossible

[ergonomic]

Using Euler's formula is easy, trivial.

[mrjnutube]

video starts very well, and i was going to give 5 stars. The he got lost with an extremely poor diagram seeming to show a not so horizontal cord C and something

[bruceedward]

The proof is poorly executed, you need to clearly mention the parameters of what is what, you need to tell clearly right angle relationship in triangle to execute phythageron theorem,