filmov
tv
Particle sliding down a sphere: when does it lose contact?

Показать описание
About me: I studied Physics at the University of Cambridge, then stayed on to get a PhD in Astronomy. During my PhD, I also spent four years teaching Physics undergraduates at the university.
#physics #maths #math #mechanics #dynamics #forces #resolving #particle #smooth #sphere #motion #circularmotion
Particle sliding down a sphere: when does it lose contact?
Particle sliding off a sphere, using Lagrangian mechanics
Particle sliding down a fixed sphere!/ Work and Energy/ HCVerma Q. No.60
Particle on a Sphere
A particle sliding down a hemisphere - by Lagrangian mechanics
Angle at which particle leaves sphere: force-free method
At what angle with a frictionless puck leave the surface of an inverted bowl?
A particle slides on the surface of a fixed smooth sphere starting from the topmost pont. Find t...
Particle leaving sphere immediately: force-free method
Block sliding off a fixed sphere
Ball rolling down a rough sphere: when does it lose contact?
Particle On A Sphere | Physical Chemistry II | 7.4
Magnetic Accelerators | Magnetic Games
Angular Momentum Demo Arms IN vs OUT
Sliding of a particle on a smooth sphere, H.C. Verma Problem Circular motion, cons. of energy
Particle slides down the surface of a smooth fixed sphere of radius r starting from rest at the ...
A particle is kept at rest at the top of a sphere of diameter 42 m. When WEP DTS 08 Q4
A particle slides on the surface of a fixed smooth sphere starting from the topmost point. Find t...
Particles moving in circles on surface of sphere
Potential energy of a sphere: an unconventional method
Adv Illustrations – A Ball Sliding inside a Cylindrical Groove | System of Particles #4 for JEE Adv...
Mount Everest is Completely Covered with Human Corpses #science #sciencefacts
What angle does a block leave the surface of a sphere - using Lagrange Multipliers
Anti Gravity Wheel?? ..#theoryofphysics #physics #anubhavsir
Комментарии
 0:11:43
0:11:43
 0:14:52
0:14:52
 0:07:36
0:07:36
 0:19:56
0:19:56
 0:07:03
0:07:03
 0:09:45
0:09:45
 0:08:51
0:08:51
 0:05:37
0:05:37
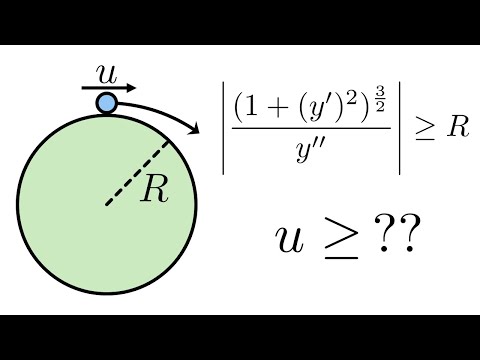 0:06:37
0:06:37
 0:16:08
0:16:08
 0:15:31
0:15:31
 0:07:14
0:07:14
 0:04:29
0:04:29
 0:00:47
0:00:47
 0:05:52
0:05:52
 0:14:53
0:14:53
 0:02:12
0:02:12
 0:05:54
0:05:54
 0:00:09
0:00:09
 0:06:42
0:06:42
 0:02:51
0:02:51
 0:00:23
0:00:23
 0:33:54
0:33:54
 0:01:00
0:01:00