filmov
tv
A gem of an integral from the JEE advanced calculus exam
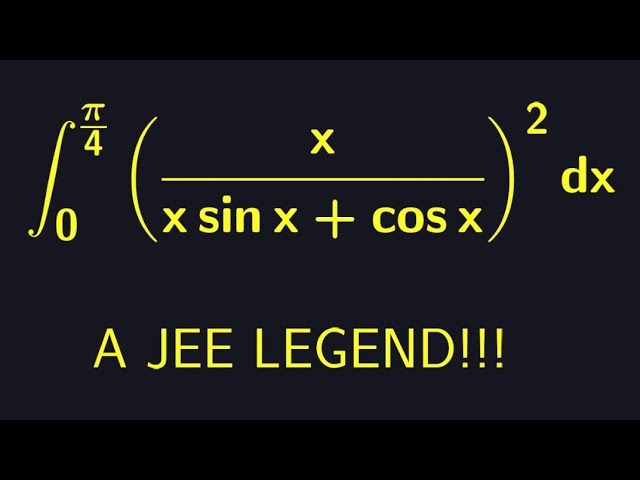
Показать описание
Here's my first integral from the Indian JEE advanced calculus exam. Solution development involved using some nice trigonometric tricks and integration by parts.
A gem of an integral from the JEE advanced calculus exam
HOW INTEGRATION WORKS. A GEM FUSION? All About Alters 7 | Dissociative Identity Disorder
Ex: Infinite Series - Integral Test (Rational Function and Divergent)
The Ultimate Hidden Gem Driver - Flawless Look, Incredible Feel - Darkspeed #golf #golfequipment
Printfull Integration In GEM Software
itslearning Assignments - Step 11 - Google Integration - GEM - BCSC
Saying Goodbye to a True Gem!
GEM-FIX quick integration with Labor guide software for the automotive industry make you save time!
RubyConf 2021 - How to Make a Gem of a Gem by Justin Searls
Sequence & Series (SS 128-Gem-35)
Salt: The History of a Hidden Gem from Ancient Currency to Culinary Essential! #Shorts #RomanEmpire
#jwelcart #earrings #jewelleryjewellery #gift #jewell #jaipur #jewels #india #amethyst #silver #gem
Gem Skull Pendant Carved from Amethyst, Black Obsidian, and other materials
Sequence & Series (SS-149-Gem 33)
SECS/GEM Software Integration for MRD XL
Integral & Approximation Gem (Fanmade - Credits To Soup Earth Society)
#09 ~ Hide app integration API Keys with the Dotenv Gem
#jwelcart #jewelleryjewellery #earrings #gift #jewell #jaipur #jewels #india #amethyst #silver #gem
CARQUEST Weblink catalog integration with GEM-CAR shop management software
Explore Wat Phutthaisawan: A Historic Gem of Thailand
PILOT Rover DbW integration Polaris GEM
R.I.P Sir Ratan Tata ! India has Lost a Gem, Legend & inspiration to all' #ratantata #indi...
Gem CRM: Your ATS' Best Friend
#jwelcart #earrings #jewelleryjewellery #gift #jewell #jaipur #jewels #india #amethyst #silver #gem
Комментарии
 0:09:34
0:09:34
 0:16:11
0:16:11
 0:04:39
0:04:39
 0:00:32
0:00:32
 0:06:00
0:06:00
 0:01:48
0:01:48
 0:00:37
0:00:37
 0:00:21
0:00:21
 0:31:00
0:31:00
 0:01:57
0:01:57
 0:01:01
0:01:01
 0:00:06
0:00:06
 0:00:18
0:00:18
 0:03:35
0:03:35
 0:06:12
0:06:12
 0:00:03
0:00:03
 0:05:02
0:05:02
 0:00:05
0:00:05
 0:03:26
0:03:26
 0:00:17
0:00:17
 0:00:29
0:00:29
 0:00:55
0:00:55
 0:00:41
0:00:41
 0:00:06
0:00:06