filmov
tv
Worked example: Derivative of ÃÂ(3x_-x) using the chain rule | AP Calculus AB | Khan Academy

Показать описание
f(x)=Ã(3x_-x) is a composition of the functions Ãx and 3x_-x, and therefore we can differentiate it using the chain rule. Created by Sal Khan.
AP Calculus AB on Khan Academy: Bill Scott uses Khan Academy to teach AP Calculus at Phillips Academy in Andover, Massachusetts, and heÕs part of the teaching team that helped develop Khan AcademyÕs AP lessons. Phillips Academy was one of the first schools to teach AP nearly 60 years ago.
For free. For everyone. Forever. #YouCanLearnAnything
Vector Differentiation (Part-3)
Problem 3.5 - Observables ⇢ Hermitian Conjugates: Introduction to Quantum Mechanics
Factor and Solve Quadratic Equations - Leading Coefficient Other Than One - Quick and Easy Method!
Position vector valued functions | Multivariable Calculus | Khan Academy
How to Find a Definite Integral using Riemann Sums and the Limit Definition: Quadratic Example
Proof by Induction : Sum of series ∑r² | ExamSolutions
Factoring: Trinomials with non-1 leading coefficient
Vectors | Scalar & Cross product | Derivative of vector function | Gradient | Directional Deriva...
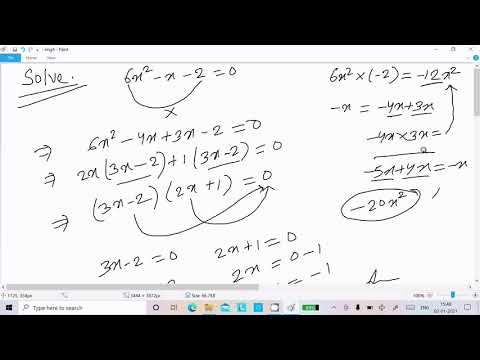
Solve 6x^2 - x - 2 = 0
Factoring Trinomials that have a Leading Coefficient Greater than One - J. Cornett
Algebra of Operators in Quantum Mechanics | Properties | Addition subtraction and Multiplication
The Exact Value for Tangent of 18 Degrees, tan(18)
Vector Calculus 2.O | Gradient - Directional Derivative | Concept & Questions by GP Sir
Engg. Maths I Directional Derivative I Vector Differentiation I By Prof. Sagar Wabale
Engineering Mathematics III Vector differentiation LECTURE 1
Vertical tangent and cusp
If unit vectors `hat(a)` and `hat(b)` are inclined at angle `theta`, then prove that
FM2 4 2a 3 t=tan0 5x
Commutative and non Commutative operators in Quantum Mechanics along with Solved Numerical Problems
Lecture2 Five Critical Operator Identities for Quantum Mechanics
dynamics problems contains differentiation and integration
PHYS 390 Class 4: TISE, Harmonic Oscillator (algebraic approach)
Double Integration Method | Slope & Deflection Of Cantilever Beams | T.O.S
Position and Momentum Operators in Quantum Mechanics
Комментарии
 0:13:29
0:13:29
 0:12:03
0:12:03
 0:03:46
0:03:46
 0:07:05
0:07:05
 0:13:18
0:13:18
 0:08:16
0:08:16
 0:10:03
0:10:03
 0:53:52
0:53:52
 0:03:14
0:03:14
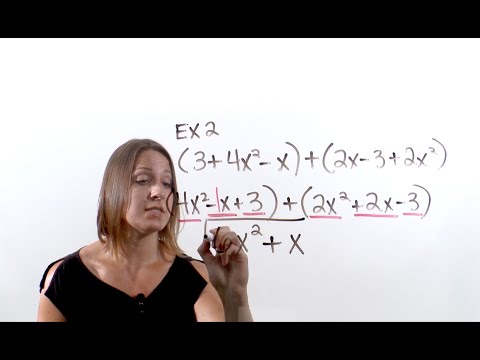 0:13:30
0:13:30
 0:12:45
0:12:45
 0:13:58
0:13:58
 0:17:42
0:17:42
 0:05:10
0:05:10
 0:40:23
0:40:23
 0:05:17
0:05:17
 0:02:11
0:02:11
 0:24:05
0:24:05
 0:09:40
0:09:40
 0:38:57
0:38:57
 0:28:40
0:28:40
 0:29:27
0:29:27
 0:15:51
0:15:51
 0:26:05
0:26:05