filmov
tv
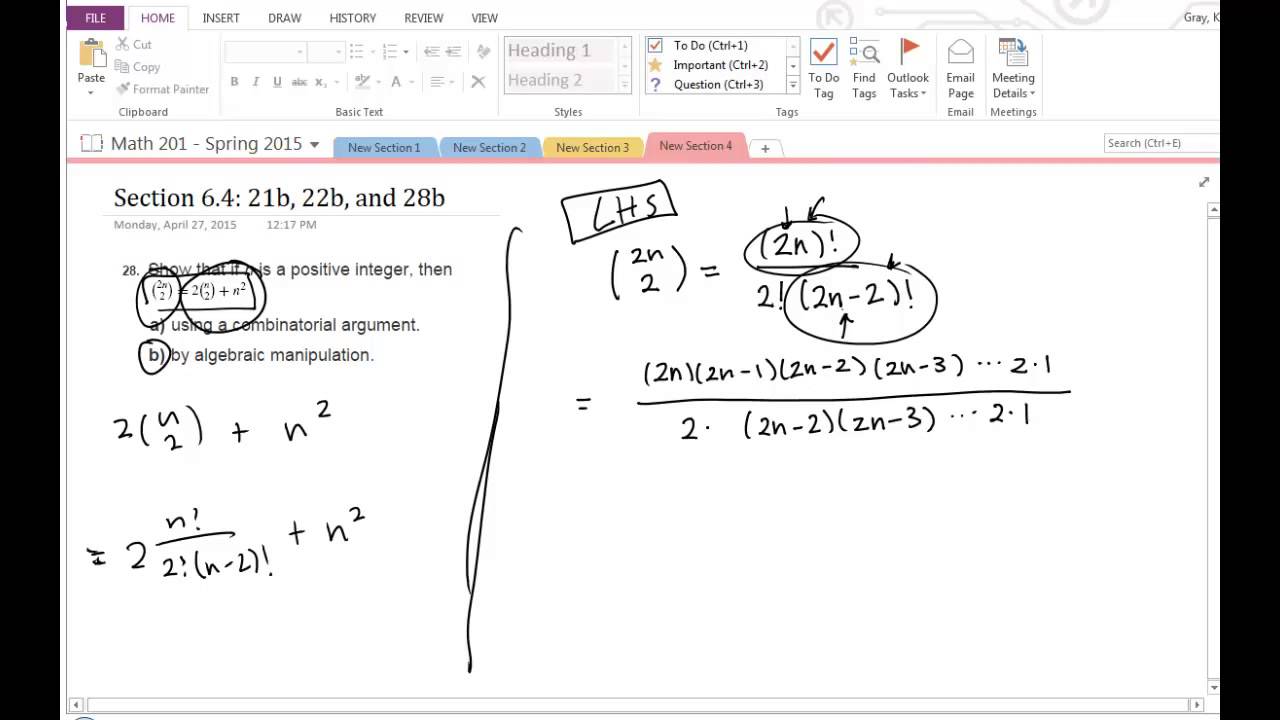
Proof that C(2n, 2)=2*C(n,2)+n^2
Показать описание
Algebraic proof of this equality
0:07:31
Proof that C(2n, 2)=2*C(n,2)+n^2
0:03:30
Combinatorial Proof : C(2n,2) = 2*C(n,2) + n^2 | Combinatorial Proofs-3
0:07:58
Prove: C(2n,n) = C(n,0)^2 + C(n,1)^2 +...+ C(n,n)^2 | Combinatorics
0:18:24
Combinatorial Proof about C(2n,n)
0:01:00
Prove that 2n choose n is always even
0:12:27
Induction Inequality Proof Example 6: [2^(2n)]*(n!)^2 ≥ (2n)!
0:05:04
11.g) Prove that: C0²+C1²+C2²+C3²+...+Cn²=(2n)!/(n!)² If (1+x)ⁿ=C0+C1x+C2x²+...+Cnxⁿ Binomial NEB 12...
0:02:40
Prove that : `(C(2n,n))/(n+1)` is an integer
0:04:04
Істер Вправа 239. Алгебра 7 клас
0:04:00
6.C02+C12+C22+………………………+Cn2=(2n)!/(n!)^2 I HSC & Admission I 1 minute mcq
0:15:46
1.8.1 Asymptotic Notations Big Oh - Omega - Theta #1
0:10:40
Prove equation C(2n, n) = Sum C(n, i)^2 for i = 1, 2,... n
0:07:57
nC0 2nCn - nC1 (2n-2)Cn + nC2 (2n-4)Cn.............. equals to ?
0:07:08
Learn how to use mathematical induction to prove a formula
0:07:26
2.3.2 Recurrence Relation Dividing [ T(n)=T(n/2)+ n]. #2
0:05:30
Derivation | Formula | Sum of first n squares or square numbers 1^2 + 2^2 + 3^2 + 4^2 +...n^2
0:11:17
Factorials Explained!
0:07:39
(n+1)^2+(n+2)^2 +..... +(2n)^2= n(2n+1)(7n+1)/6 || Principal of Mathematical Induction | CBCS/GU
0:08:16
Proof by Induction : Sum of series ∑r² | ExamSolutions
0:08:57
L-2.4: Recurrence Relation [ T(n)= 2T(n/2) +n] | Substitution Method | Algorithm
0:07:52
Theory of Computation: PDA Example (a^n b^2n)
0:09:20
Inequality Mathematical Induction Proof: 2^n greater than n^2
0:03:01
if `.^(2n)C_(2):^(n)C_(2)=9:2 and .^(n)C_(r)=10`, then r is equal to
0:07:12
11.f) Prove that: C0C1+C1Cn-1+...+CnC0=(2n)!/(n!n!) If (1+x)ⁿ=C0+C1x+C2x²+...+Cnxⁿ. Binomial NEB 12...
Комментарии