Variational Multiscale Modeling & Memory Effects in Turbulent Flow Simulations

Eric Parish PhD Dissertation Defense (May the fourth, 2018)

Effective computational models of multiscale problems have to account for the impact of unresolved physics on the resolved scales. This dissertation advances our fundamental understanding of multiscale models and develops a mathematically rigorous closure modeling framework by combining the Mori-Zwanzig (MZ) formalism of Statistical Mechanics with the variational multiscale (VMS) method. This approach leverages scale-separation projectors as well as phase-space projectors to provide a systematic modeling approach that is applicable to complex non-linear partial differential equations.

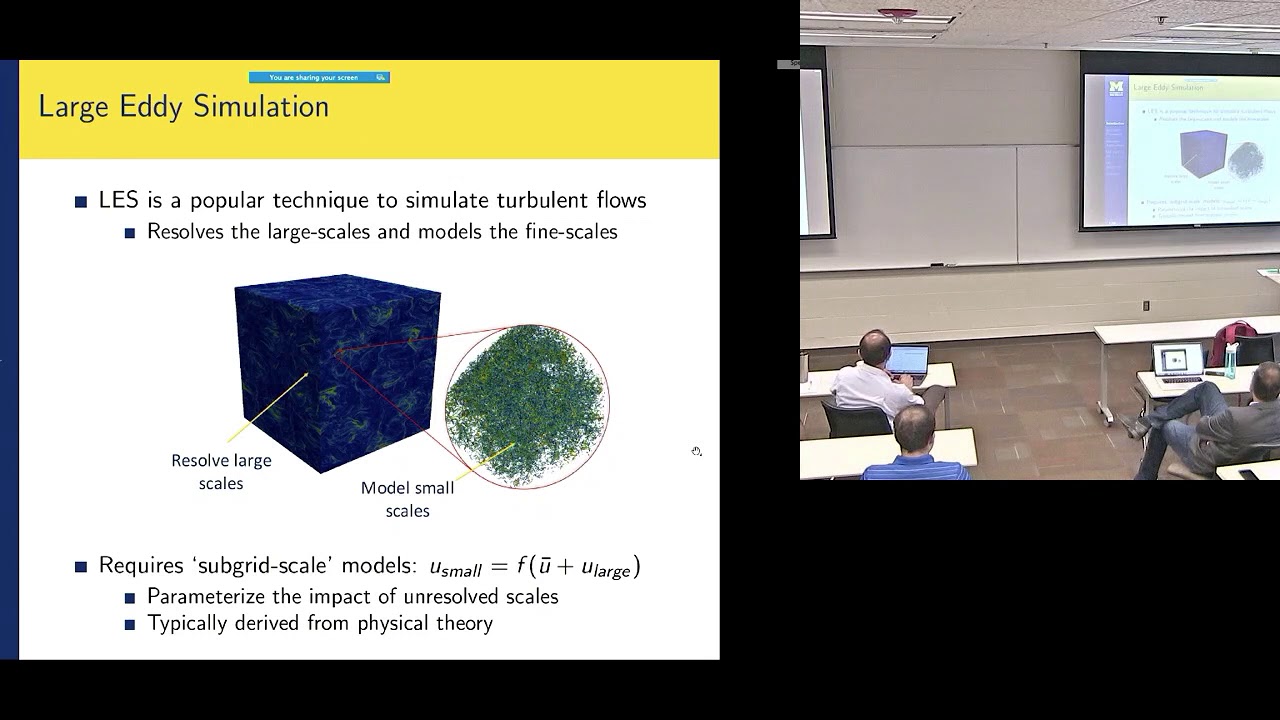
The MZ-VMS framework is investigated in the context of turbulent flows. Spectral as well as continuous and discontinuous finite element methods are considered. The MZ-VMS framework leads to a closure term that is non-local in time and appears as a convolution or memory integral. The resulting non-Markovian system is used as a starting point for model development. Several new insights are uncovered: It is shown that unresolved scales lead to memory effects that are driven by an orthogonal projection of the coarse-scale residual and, in the case of finite elements, inter-element jumps. Connections between MZ-based methods, artificial viscosity, and VMS models are explored.

The MZ-VMS framework is investigated in the context of turbulent flows. Large eddy simulations of Burgers' equation, turbulent flows, and magnetohydrodynamic turbulence using spectral and discontinuous Galerkin methods are explored. In the spectral method case, we show that MZ-VMS models lead to substantial improvements in the prediction of coarse-grained quantities of interest. Applications to discontinuous Galerkin methods show that modern flux schemes can inherently capture memory effects, and that it is possible to guarantee non-linear stability and conservation via the MZ-VMS approach. We conclude by demonstrating how ideas from MZ-VMS can be adapted for shock-capturing and filtering methods.