filmov
tv
10. Depth-First Search

Показать описание
MIT 6.006 Introduction to Algorithms, Spring 2020
Instructor: Justin Solomon
This class builds on the previous lecture of breadth-first search (BFS) by introducing depth-first search (DFS) and full-BFS and full-DFS. The lecture continues with topological sorts and cycle detection.
License: Creative Commons BY-NC-SA
Instructor: Justin Solomon
This class builds on the previous lecture of breadth-first search (BFS) by introducing depth-first search (DFS) and full-BFS and full-DFS. The lecture continues with topological sorts and cycle detection.
License: Creative Commons BY-NC-SA
10. Depth-First Search
5.1 Graph Traversals - BFS & DFS -Breadth First Search and Depth First Search
Depth First Search Algorithm
Depth First Search Algorithm | Graph Theory
Depth First Search
Learn Depth First Search in 7 minutes ⬇️
6.2 BFS and DFS Graph Traversals| Breadth First Search and Depth First Search | Data structures
Depth First Search (DFS) Explained: Algorithm, Examples, and Code
Depth First Search (DFS) with example | Uninformed Search | Artificial Intelligence
Depth-First Traversals
Depth First Search (DFS) Algorithm Explained
Top 5 Most Common Graph Algorithms for Coding Interviews
Depth First Search (DFS) Algorithm Python Implementation
Binary tree traversal - breadth-first and depth-first strategies
Breadth First Search Algorithm | Shortest Path | Graph Theory
L-4.15: BFS & DFS | Breadth First Search | Depth First Search | Graph Traversing | DAA
Graph Search Algorithms in 100 Seconds - And Beyond with JS
I gave 127 interviews. Top 5 Algorithms they asked me.
Iterative Deepening
Graphs - Depth First Search
Depth First Search || Tamil || 3mins
Breadth First Search (BFS): Visualized and Explained
Graph Searching 5 Performing DFS by Hand
Clone Graph - Depth First Search - Leetcode 133
Комментарии
 0:52:23
0:52:23
 0:18:31
0:18:31
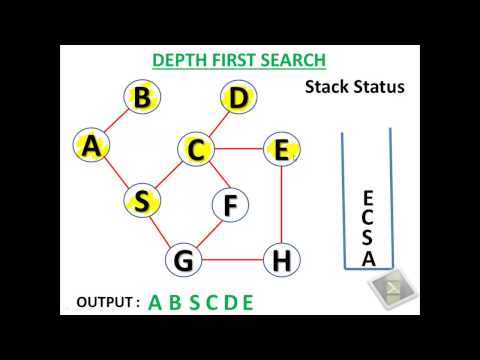 0:03:47
0:03:47
 0:10:20
0:10:20
 0:07:16
0:07:16
 0:07:41
0:07:41
 0:20:27
0:20:27
 0:20:52
0:20:52
 0:09:13
0:09:13
 0:02:36
0:02:36
 0:00:34
0:00:34
 0:13:01
0:13:01
 0:00:24
0:00:24
 0:11:54
0:11:54
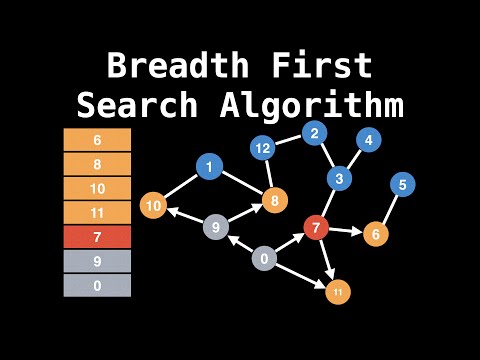 0:07:23
0:07:23
 0:11:16
0:11:16
 0:10:30
0:10:30
 0:08:36
0:08:36
 0:03:40
0:03:40
 0:06:25
0:06:25
 0:02:52
0:02:52
 0:10:41
0:10:41
 0:06:46
0:06:46
 0:11:48
0:11:48