mod12lec72 - Locally compact Hausdorff spaces

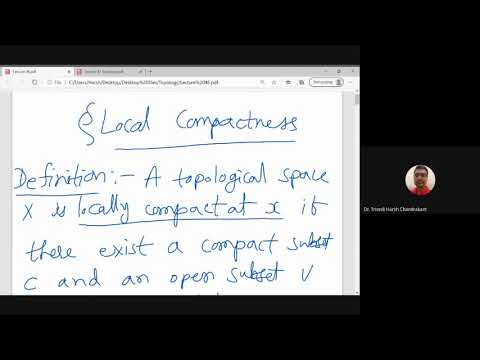
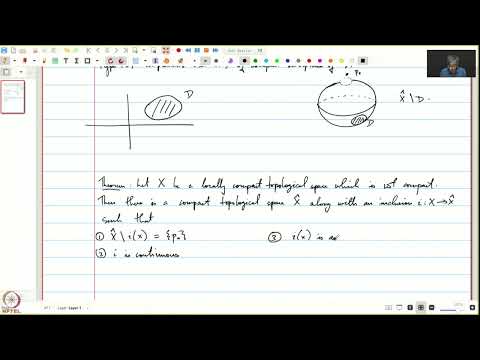
In order to find a converse to the forward implication of Arzelà- Ascoli theorem proved in the last lecture, we restrict to the case when X is a locally compact Hausdorff (LCH) space. We therefore study briefly the definition and basic properties of LCH spaces. We prove that LCH spaces are regular and Baire spaces, by viewing such a space inside a compact Hausdorff space as an open dense subspace. This construction is called the one-point compactification of X.

[nishantsutar]

does the construction also works if X itself is compact.