filmov
tv
Quotient Rule vs. L'Hospital's Rule
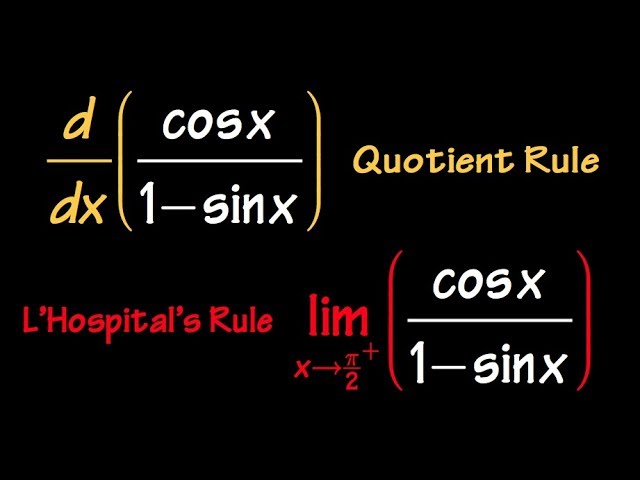
Показать описание
Derivative of cos(x)/(1-sin(x)) vs. Limit of cos(x)/(1-sin(x)) as x goes to pi/2, Example of Quotient Rule vs. L'Hospital's Rule!
Please subscribe for more math content!
Check out my site & social media
Thank you for your support!
blackpenredpen | 曹老師
Please subscribe for more math content!
Check out my site & social media
Thank you for your support!
blackpenredpen | 曹老師
Quotient Rule vs. L'Hospital's Rule
L'Hospital's Rule 🤺vs.🤺 Quotient Rule... Don't mix them up! 👨🍳 #apcalculus #apcalc #...
L'hopital's rule
L'Hospital's Rule, Derivative, Limits, Example - AP Calculus BC
L'hospitals Rule in 57 Seconds!! (Calculus)
l'Hôpital's Rule
Calculus - L'Hospital's Rule - Quotient
L'Hospital's Rule | Indeterminate Form Type 0/0 | y=(8^t - 5^t)/t
Calculus 2 Exam Review Part6
L'Hospital's Rule, Derivative, Limits, Example - AP Calculus BC
2 2 2 chapter 2 sum & difference, product and quotient rules
This is a very famous limit
08.7 - L'Hopital's Rule (product & quotient forms)
L'Hospital's Rule | Indeterminate Form Type Infinity/Infinity | y=[(lnx)^2]/x
Use of L 'Hospital's Rule I Limits 🔥🔥 #shorts #maths
L'Hospital's Rule, Derivative, Limits, Example - AP Calculus BC
The limit is the limit is the limit is the limit
also works for infinity/infinity! #lhospital #apcalc #calculus #apexams #limits
4_7 l'Hospital's Rule Introduction
L'Hospital's Rule | Indeterminate Form Type Infinity*0 | y=sqrt(x)*e^(-x/2)
L’HOSPITAL'S RULE - HOW TO - With Examples
Limits Made Easy: L'Hopital's Rule
L'Hospital's Rule | Indeterminate Form Type 0/0 | y=(x*3^x)/[(3^x)-1]
L'Hospital's Rule
Комментарии
 0:06:28
0:06:28
 0:00:43
0:00:43
 0:13:09
0:13:09
 0:00:22
0:00:22
 0:00:57
0:00:57
 0:26:00
0:26:00
 0:09:28
0:09:28
 0:01:00
0:01:00
 5:47:36
5:47:36
 0:00:29
0:00:29
 0:10:09
0:10:09
 0:00:48
0:00:48
 0:17:12
0:17:12
 0:01:00
0:01:00
 0:00:26
0:00:26
 0:00:41
0:00:41
 0:00:14
0:00:14
 0:00:40
0:00:40
 0:27:44
0:27:44
 0:01:00
0:01:00
 0:16:35
0:16:35
 0:03:14
0:03:14
 0:01:00
0:01:00
 0:06:42
0:06:42