Recursive Digit Sum Java Coding Challenge | HackerRank | Edabit | How'd You Code That?

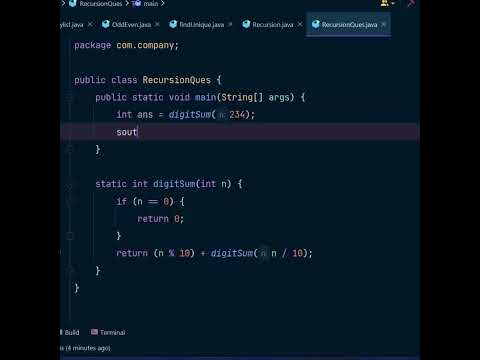
We define super digit of an integer `x` using the following rules:
Given an integer, we need to find the super digit of the integer.
* If `x` has only `1` digit, then its super digit is `x`.
* Otherwise, the super digit of `x` is equal to the super digit of the sum of the digits of `x`.
For example, the super digit of `x` will be calculated as:
super_digit(9875) 9+8+7+5 = 29
super_digit(29) 2 + 9 = 11
super_digit(11) 1 + 1 = 2
super_digit(2) = 2
You are given two numbers `n` and `k`. The number `p` is created by concatenating the string times. Continuing the above example where `n = 9875`, assume your value `k=4`. Your initial `p = 9875 9875 9875 9875` (spaces added for clarity).
superDigit(p) = superDigit(9875987598759875)
5+7+8+9+5+7+8+9+5+7+8+9+5+7+8+9 = 116
superDigit(p) = superDigit(116)
1+1+6 = 8
superDigit(p) = superDigit(8)
All of the digits of `p` sum to `116`. The digits of `116` sum to `8`. `8` is only one digit, so it's the super digit.

Complete the superDigit() method. It must return the calculated super digit as an integer.
superDigit has the following parameter(s):
* n: a string representation of an integer
* k: an integer, the times to concatenate `n` to make `p`

Song: Fresh - Ikson (Vlog No Copyright Music)
Music promoted by Vlog No Copyright Music.