filmov
tv
Factorial Differentiation: How to differentiate x!
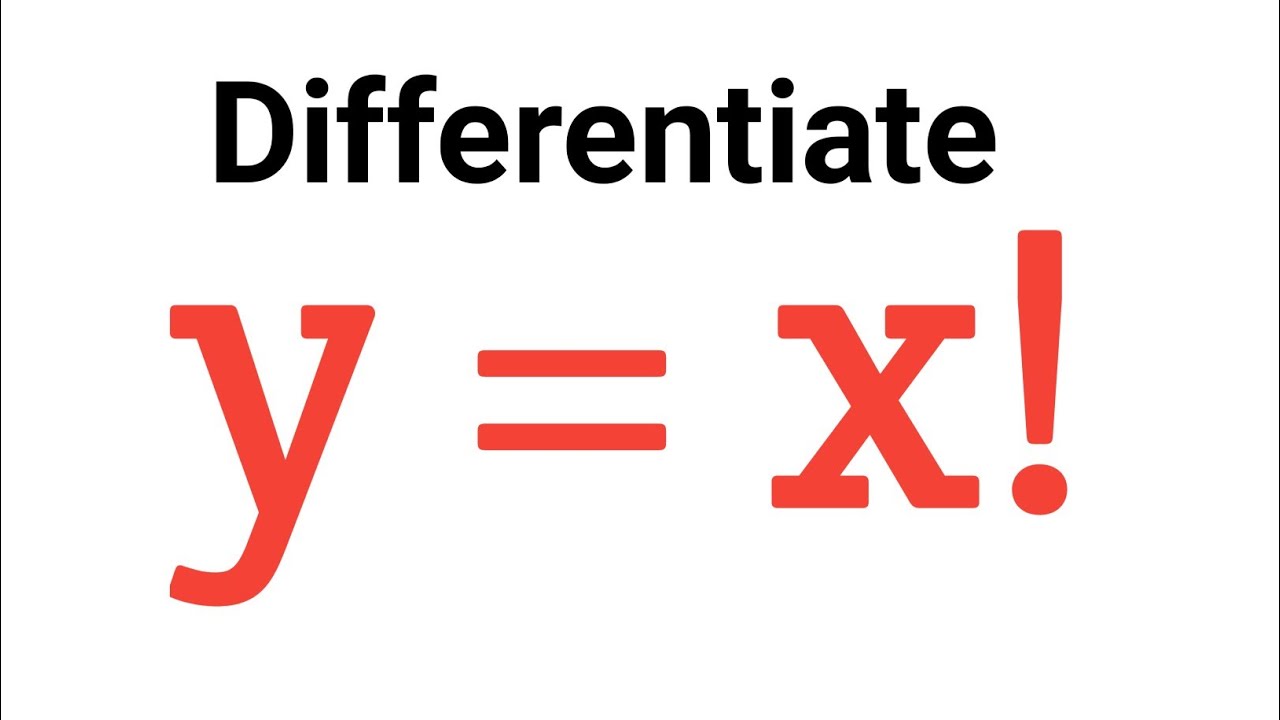
Показать описание
Differentiation of factorial functions. Differentiate x factorial. Differentiate x! If y = x! find dy/dx.
I Found Out How to Differentiate Factorials!
Derivative of The Factorial Function
Factorial Differentiation: How to differentiate x!
WAIT, WHAT?! DIFFERENTIATING x FACTORIAL x! - Introducing the Digamma Function
Derivative of The Factorial Function
How to Take the Factorial of Any Number
Derivative of a factorial (5 Solutions!!)
How REAL Men Integrate Functions
Differentiation VS Factorial #shorts #mathematics #challenge #viral #factorial #differentiation
derivative of the factorial vs factorial of the derivative
Fractional order derivative of a function & fractional numbers' factorial.
Extending the FACTORIAL! Gamma function derived in 60 seconds!
Differentiating power series | Series | AP Calculus BC | Khan Academy
Derivatives of Exponential Functions
A nice limit involving derivative of x factorial
Product Rule For Derivatives
Best way to evaluate factorial problem.
Wow,r times derivative of n factorial
100 calculus derivatives (ultimate derivative tutorial)
pi-th derivative of x^pi
Derivatives of Logarithmic and Exponential Functions
The Unbelievable Transformation: Finding the Factorial of the Derivative!
the untaught differentiation formula, the derivative of (f(x))^g(x), calculus 1 tutorial
How to do this Factorial related Differentiation Question
Комментарии
 0:04:06
0:04:06
 0:06:47
0:06:47
 0:07:16
0:07:16
 0:18:05
0:18:05
 0:02:26
0:02:26
 0:26:31
0:26:31
 0:04:41
0:04:41
 0:00:35
0:00:35
 0:00:11
0:00:11
 0:06:51
0:06:51
 0:14:51
0:14:51
 0:00:56
0:00:56
 0:08:01
0:08:01
 0:12:03
0:12:03
 0:04:57
0:04:57
 0:11:11
0:11:11
 0:00:16
0:00:16
 0:00:10
0:00:10
 6:38:13
6:38:13
 0:09:25
0:09:25
 0:08:41
0:08:41
 0:15:31
0:15:31
 0:07:06
0:07:06
 0:04:09
0:04:09