filmov
tv
Lecture 9(A): Euclidean Space

Показать описание
Norm, distance, Triangle Inequality, dot product.
Lecture 9(A): Euclidean Space
Real Analysis Lecture 9 | Euclidean Space | Euclidean n Space | BS / MSc Mathematics Lectures
Lecture 9(B): Euclidean Space: Cauchy-Schwarz and Triangle inequalities, dot product, hyperplanes.
Euclidean Spaces
Differential Geometry: Lecture 9 part 1: Euclidean geometry of Rn
ENB339 lecture 9: Image geometry and planar homography
Euclidean Space, Locally Euclidean Space, and Manifolds
This chapter closes now, for the next one to begin. 🥂✨.#iitbombay #convocation
Euclidean Space
Euclidean Spaces
Why greatest Mathematicians are not trying to prove Riemann Hypothesis? || #short #terencetao #maths
Lecture 10(A): Euclidean Space: Neighborhoods, Open and Closed Sets
09 euclidean space and vector
Three Dimensional Euclidean Space
Multivariable Functions Lecture 1 Part 1: Functions between Euclidean Spaces
Euclidean Space Span Clip 1
Euclidean spaces and fields defined on them.
Manifolds 9 | Locally Euclidean Spaces [dark version]
What is Euclidean Space & Inner Product
Functional Analysis 9 | Examples of Inner Products and Hilbert Spaces [dark version]
Welcome to Euclidean Space
What is a Manifold? Lesson 9: The Tangent Space-Definition
MAT221 Lecture 2 Part III: Euclidean Spaces
Euclidean Space Lecture-1
Комментарии
 0:31:04
0:31:04
 0:07:57
0:07:57
 0:27:25
0:27:25
 0:05:46
0:05:46
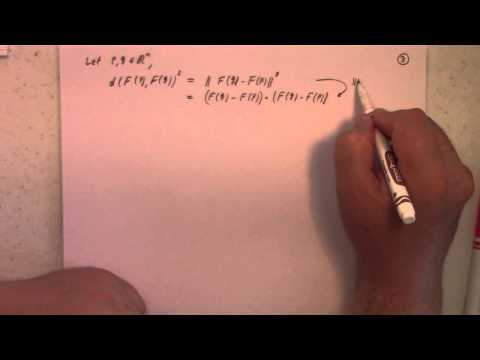 0:25:00
0:25:00
 0:35:23
0:35:23
 0:09:38
0:09:38
 0:00:16
0:00:16
 0:07:37
0:07:37
 0:34:18
0:34:18
 0:00:38
0:00:38
 0:28:32
0:28:32
 0:07:24
0:07:24
 0:06:23
0:06:23
 0:08:14
0:08:14
 0:14:59
0:14:59
 0:00:12
0:00:12
 0:07:57
0:07:57
 0:01:28
0:01:28
 0:06:53
0:06:53
 0:06:48
0:06:48
 1:23:35
1:23:35
 0:10:10
0:10:10
 0:27:02
0:27:02