filmov
tv
Separable differential equation 2.2#17

Показать описание
Learn how to solve a separable differential equation. This is usually the first kind of differential equations that we learn in an ordinary differential equations class.
To learn how to solve different types of differential equations:
For more calculus & differential equation tutorials, check out @justcalculus
#DifferentialEquations
To learn how to solve different types of differential equations:
For more calculus & differential equation tutorials, check out @justcalculus
#DifferentialEquations
Separable differential equation 2.2#17
Separable First Order Differential Equations - Basic Introduction
17 Hmk Separable Differential Equations Q2g
4-18-17 Separable Differential Equations Part 2
Solving Differential Equations (separable)
Solving a Separable Differential Equation #2 - Differential Equations
Differential Equations: Lecture 2.2 Separable Equations
Separable Differential Equations Ft. The Math Sorcerer
Vector Algebra | Class 12 - NCERT Math | Ex-10.4 - Q1 & Q2 #class12th | part-1
Separable differential equations P. 391 #17
Separable Differential Equations of the type F(x)G(y)dx + f(x)g(y) = 0 (MM-9.2-1)
9.3.1 Solve Separable Differential Equation
Separable Differential Equations of the type F(x)G(y)dx + f(x)g(y) = 0 (MM-9.2-17)
Separable differential equation with initial conditions: dy/dx=xe^-x/y^2 with integration by parts.
MATH 2414 - Differential Equations (2): Separable Differential Equations
Differential Equation |Differential Equation First order|Separable|Order|Degree Lecture12 qstn 17,18
First Order Differential Equations: Separable Differential Equations 2
Separable differential equation, 2.2#24
How to solve separable differential equations (6 examples, calculus 2)
2.2.2 Separable Homogeneous First Order Equations
Solving separable differential equations (Part 2)
Separable Differential Equations Ex 2
Differential Equations: Variable Separable Method -- Introduction with an Example
Separable Differential Equation (introduction & example)
Комментарии
 0:07:25
0:07:25
 0:10:42
0:10:42
 0:06:56
0:06:56
 0:15:20
0:15:20
 0:21:44
0:21:44
 0:01:36
0:01:36
 0:56:16
0:56:16
 0:07:24
0:07:24
 0:28:32
0:28:32
 0:03:41
0:03:41
 0:01:13
0:01:13
 0:13:07
0:13:07
 0:02:55
0:02:55
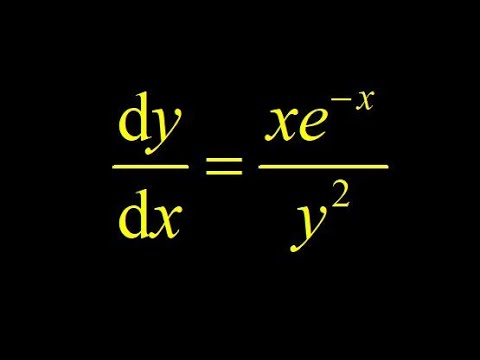 0:03:48
0:03:48
 0:11:58
0:11:58
 0:20:18
0:20:18
 0:05:16
0:05:16
 0:04:14
0:04:14
 0:27:52
0:27:52
 0:16:13
0:16:13
 0:10:58
0:10:58
 0:08:50
0:08:50
 0:05:58
0:05:58
 0:09:12
0:09:12