Introduction to additive combinatorics lecture 5.3 --- Proof of the Balog-Szemerédi theorem

Показать описание

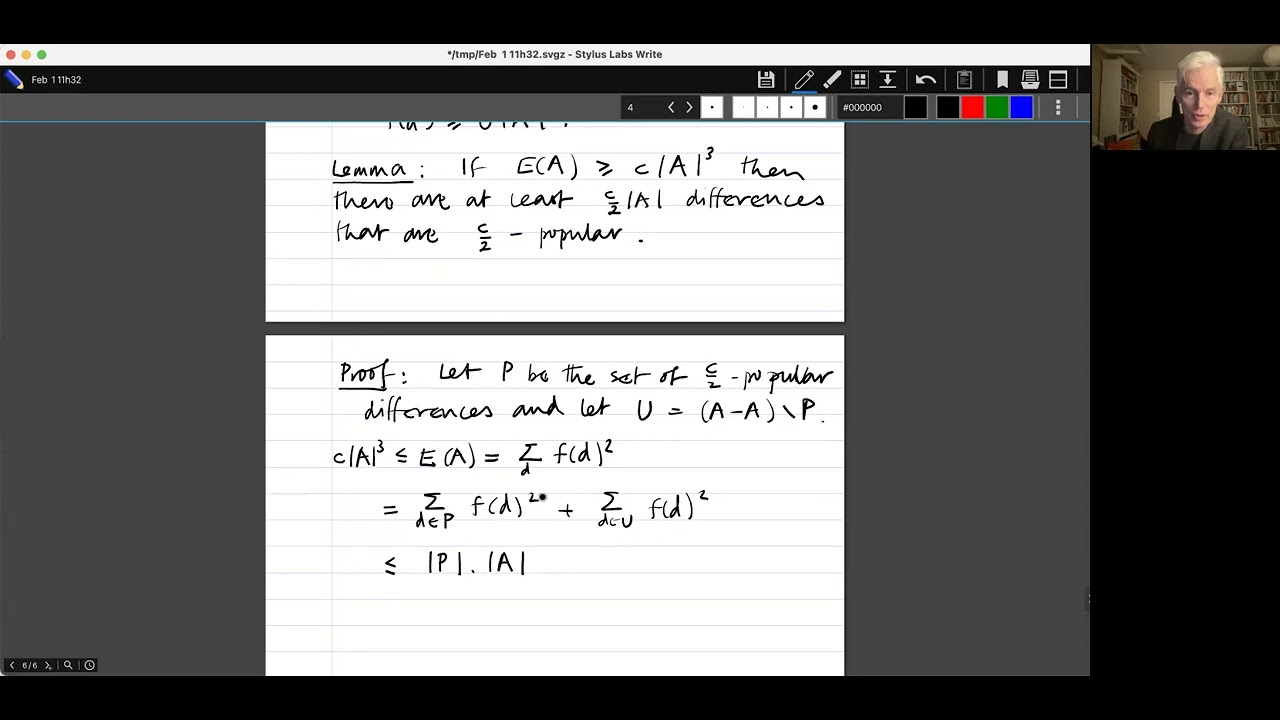
The Balog-Szemerédi theorem states that if A is a set of size n and there are at least cn^3 quadruples (x,y,z,w) in A^4 such that x-y=z-w, then A has a subset A' of size at least c' times the size of A such that A' - A' has size at most C times the size of A, where c' and C depend only on c. That is, if a set has many such quadruples, then it has a large subset with small sumset. The proof given here is a variant of an argument due to me that gave reasonable bounds (more precisely, power-type dependencies on c) for the first time.

0:00 Introduction
0:42 Recap of main result of previous video
2:40 Recap of some basic definitions and facts about additive energy
5:03 Definition of popular differences
5:59 A lower bound for the number of popular differences
12:18 Statement of the Balog-Szemerédi theorem
14:26 Proof of the theorem

Timothy Gowers

Рекомендации по теме

Introduction to additive combinatorics lecture 5.3 --- Proof of the Balog-Szemerédi theorem

Introduction to additive combinatorics lecture 1.0 --- What is additive combinatorics?

Introduction to additive combinatorics lecture 7.3 -- dual groups and the discrete Fourier transform

Pablo Shmerkin: Additive combinatorics methods in fractal geometry - lecture 2

Peter Varju: Additive combinatorics methods in fractal geometry - lecture 1

Pablo Shmerkin: Additive combinatorics methods in fractal geometry - lecture 1

Information Theory and Additive Combinatorics

MathSoc Galois LS - 'A short introduction to additive combinatorics' by Borys Kuca

Introduction to additive combinatorics lecture 8.7 --- Bohr sets and Bogolyubov's lemma.

Introduction to additive combinatorics lecture 3.7 --- using dependent random selection

Introduction to additive combinatorics lecture 13.0 --- The U2 norm and progressions of length 3.

Introduction to additive combinatorics lecture 10.1 --- the structure and properties of Bohr sets.

Introduction to additive combinatorics lecture 12.1 --- Finishing the proof of Roth's theorem

Introduction to additive combinatorics lecture 15.8 -- Using earlier tools, and a symmetry argument.

1. A bridge between graph theory and additive combinatorics

Introduction to additive combinatorics lecture 16.5 --- Szemerédi's theorem for 4APs in F_p^n.

Introduction to additive combinatorics lecture 14.6 --- The U3 norm is a norm

Introduction to additive combinatorics lecture 15.2 --- A large U3 norm leads to additive quadruples

Introduction to additive combinatorics lecture 14.0 --- The U3 norm and progressions of length 4

Peter Varju: Additive combinatorics methods in fractal geometry - lecture 2

Introduction to additive combinatorics lecture 5.8 --- Freiman homomorphisms and isomorphisms.

Peter Varju: Additive combinatorics methods in fractal geometry - lecture 3

Introduction to additive combinatorics lecture 10.8 --- A weak form of Freiman's theorem

Introduction to additive combinatorics lecture 11.2 --- Part of the proof of Roth's theorem

Pablo Shmerkin: Additive combinatorics methods in fractal geometry - lecture 3