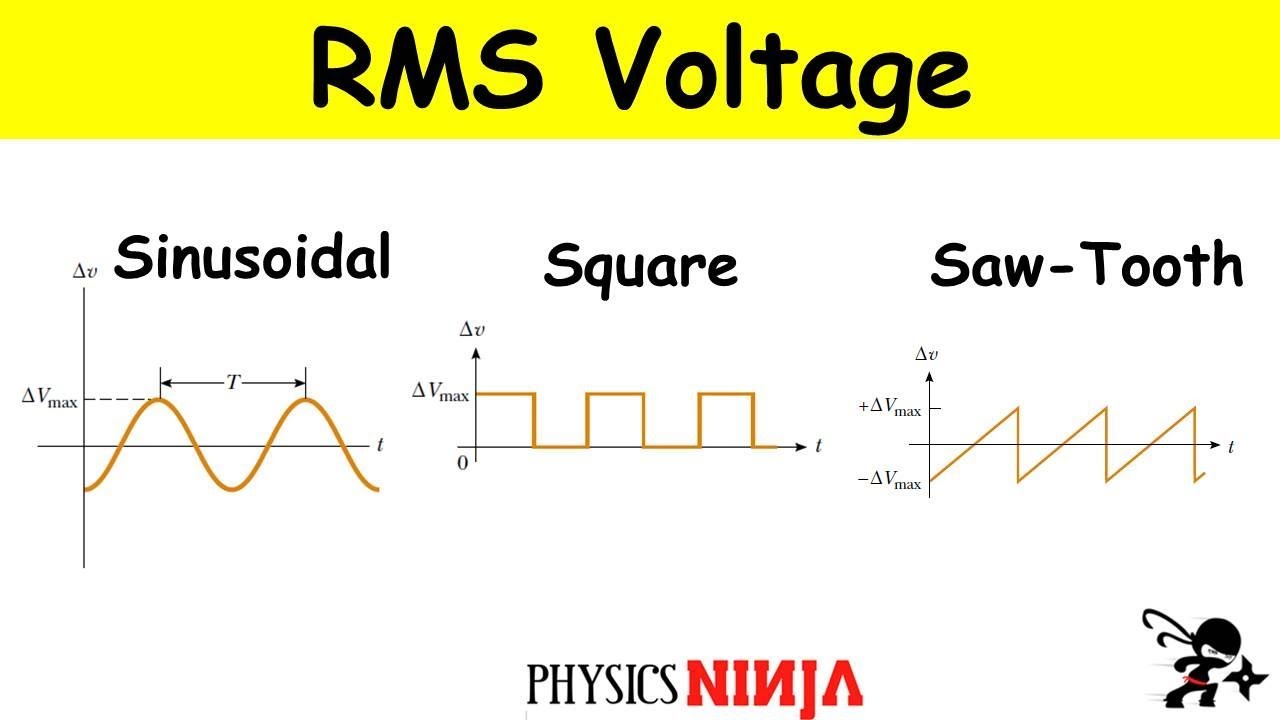
Root Mean Square (RMS) Voltage for Sinusoidal, Square ,and Sawtooth Signals

Physics Ninja shows you how to evaluate the Root Mean Squared voltage (or current) of a sinusoidal, square, and saw tooth signals.

[vlKenzo]

I’m probably a psychopath but I’m graduated and the day before I have something big at work like an important meeting or presentation I come back to videos I used to watch falling asleep before exams during my final cram. It’s extremely relaxing and keeps me fresh on topics I don’t use often

[samuelhinkle]

Thank you for an comprehendible explanation. I finally get why those calculus classes were necessary!

[JH-uxre]

Thank you so much! Very clear explanation! I learned the term in my chemistry class first and then physics, but no one explained what it is!

[gwava]

Your analysis is spot on but the motivation for rms goes like- you want a voltage value that is representative enough for energy transfer- heat in particular. For a resistor at any instant,
power = v× current
This P=vxv/R
=(v)squared/r.
Calculate average value of power over a full cycle- thats where the intergration and division by periodic time comes in.
The root now comes out of need to come up with a representative voltage for power purposes. Hence root mean square

[monolito]

Thank you so much P.N.
+
15 guys couldnt get this water clear explanation

[Omar_Alhadidi]

Thank you for this wonderful explanation

[mars]

I feel like becoming a shinobi on solving these problems
Thanks a lot amigo..

[axelmeramas]

Thank you, was really helpful. much appreciated

[ledepart.design]

Wonderful!
Greetings from Eastern Arabia

[skelly]

Thank you for the video. However, for the square wave, you don't cover the situation when the square wave becomes bipolar AND keeps the same amplitude change (+/- Vmax centered on zero). It is for this case that I am really confused because it seems that the Vrms is not the same yet the |Vavg| across the load is staying the same. In your example the |Vavg| is Vmax/2 and the same in my scenario. Any help would be appreciated.

[AmorYParodia]

Thank you for your explanation was so clear.

[adjoshi]

Thankyou, thankyou, thankyou, thankyou so much, legit life saver

[YousufAliMoiz]

Excellent Video, really appreciate for the great detail explanation.

[davidmuniz]

Thanks for an excellent explanation. I found it very helpful. I hope to see more videos of AC analysis from you.

[jimcar]

Thanks very much - I finally understand it.

[samuelmakaliki]

An alternating current varying sinusoidally with a frequency of 50 Hz
has a RMS value of 20 A. Write down the equation for the
instantaneous value and find this value at:
(a) 0.0025 s
(b) 0.0125 seconds after passing through a positive maximum value.
(c) At what time measured from a positive maximum value, will the
instantaneous current be 14.14 A?

[sridharchitta]

Current in a resistor is a start-stop motion of conduction band electrons due to their collision with the rocking lattice ions, and this causes a resistor with a sinusoidal voltage applied, to produce heat. The polarity reversals of an applied sinusoidal voltage (with the direction reversals of the applied electric field) do not affect electron collisions with the lattice ions. Electrons colliding with lattice ions from either direction will continue to produce heat and there is no cancellation of the heat developed!
Mathematically, the average value of a sinusoid is zero, and so, the average value of the current will also be zero. The average values cannot therefore represent the heat developed in a resistor with a sinusoidal current.
A resistor cannot develop heat due to a current in one half-cycle and then cool itself by a like amount of heat during the next half-cycle! It develops heat either way whether the current is positive or negative. The lattice ions vibrate from collisions irrespective of the directions in which the electrons collide with them. Therefore, since the average value is zero, it necessitates the use of the root-mean-square values of the voltage and current to compute the power, which is a statistical measure of the magnitude of a varying quantity and is the square root of the arithmetic mean of the square of the sinusoidal function.

Electrostatics and circuits belong to one science not two. To learn the operation of circuits it is instructive to understand Current, the conduction process, resistors and Voltage at the fundamental level as in the following two videos:

It is not possible in this post to discuss in more detail average and rms values. The last frame References in video #1  lists textbook 4 which discusses in detail using a unified approach sinusoidal voltage, current, their average and root mean square values.

[pedrobarbosaduarte]

Bro. This guy is the more vively version of the school teacher of south park

[MrTAM]

The sinusoidol signal is not depending on the frequency, is the square signal depending or not depending on the frequency?

[ConsertandoTudo]

The square formula is also valid for waves that does not have a 50% duty cycle ?