filmov
tv
Solving a natural logarithmic equation using the quadratic formula
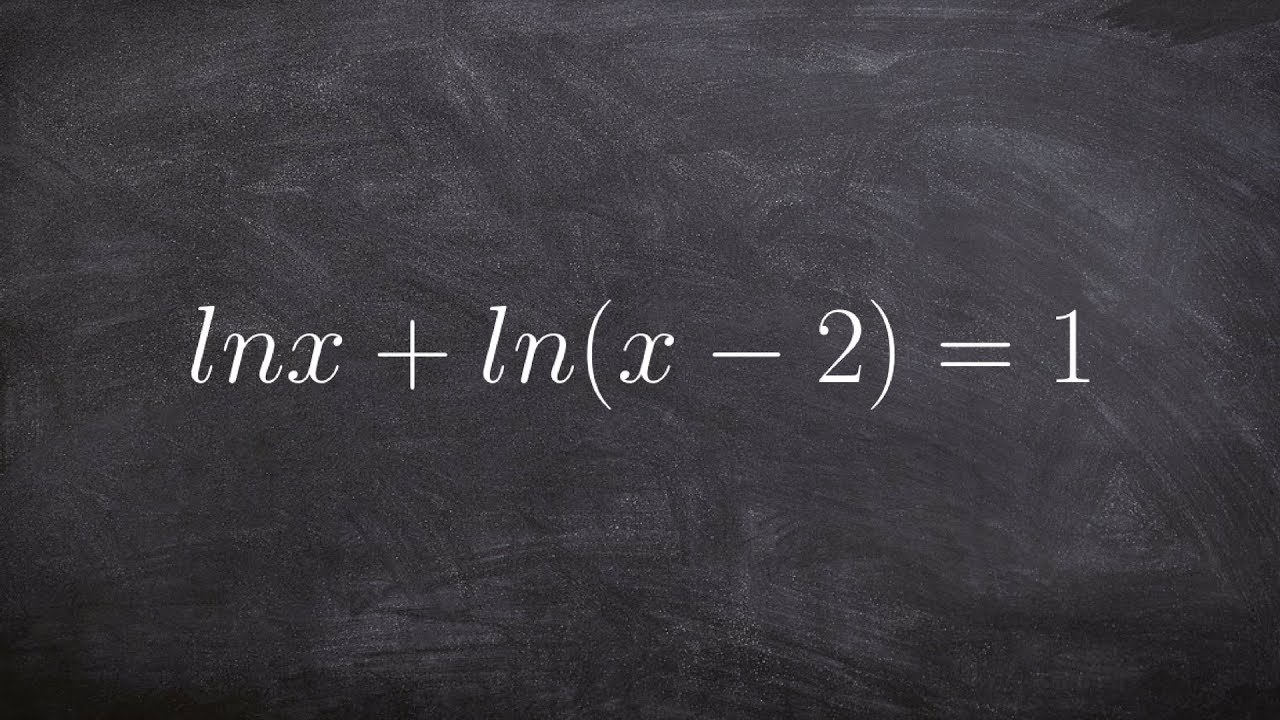
Показать описание
👉 Learn about solving logarithmic equations. Logarithmic equations are equations involving logarithms. To solve a logarithmic equation, we first use our knowledge of logarithm laws/properties to express the terms in both sides of the equality sign as single terms. Then, we equate the numbers/expressions in the logarithms and hence solve for the unknown variable. Note that the logarithms must be of the same base.
If one side of the logarithmic equation have logarithm and the other side does not have logarithm, the equation can be easily evaluated by taking the terms in both sides of the equality sign as exponents of powers with the base of the power corresponding to the base of the term having logarithm. The base of the power cancels out the logarithm and then we can evaluate the unknown variable.
Organized Videos:
✅Solve Logarithmic Equations
✅Solve Natural Logarithmic Equations
✅Solve Logarithmic Equations
✅Solve Logarithmic Equations | Learn About
✅Solve Logarithmic Equations with Multiple Logs
✅Solve Logarithmic Equations with Logs on Both Sides
Connect with me:
#Logarithms #logarithmicfunctions #brianmclogan
If one side of the logarithmic equation have logarithm and the other side does not have logarithm, the equation can be easily evaluated by taking the terms in both sides of the equality sign as exponents of powers with the base of the power corresponding to the base of the term having logarithm. The base of the power cancels out the logarithm and then we can evaluate the unknown variable.
Organized Videos:
✅Solve Logarithmic Equations
✅Solve Natural Logarithmic Equations
✅Solve Logarithmic Equations
✅Solve Logarithmic Equations | Learn About
✅Solve Logarithmic Equations with Multiple Logs
✅Solve Logarithmic Equations with Logs on Both Sides
Connect with me:
#Logarithms #logarithmicfunctions #brianmclogan
Комментарии
 0:02:49
0:02:49
 0:03:07
0:03:07
 0:01:15
0:01:15
 0:04:38
0:04:38
 0:10:34
0:10:34
 0:05:51
0:05:51
 0:25:27
0:25:27
 0:01:59
0:01:59
 0:12:10
0:12:10
 0:04:41
0:04:41
 0:01:24
0:01:24
 0:10:16
0:10:16
 0:02:23
0:02:23
 0:03:40
0:03:40
 0:12:27
0:12:27
 0:00:28
0:00:28
 0:03:13
0:03:13
 0:07:35
0:07:35
 0:04:12
0:04:12
 0:04:13
0:04:13
 0:01:39
0:01:39
 0:19:15
0:19:15
 0:04:24
0:04:24
 0:00:36
0:00:36