filmov
tv
Counting Derangements in Combinatorics
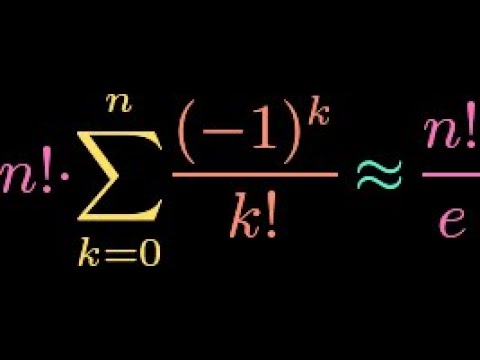
Показать описание
Derangements in combinatorics are permutations with no fixed points, meaning no element gets mapped to itself. In this video, we use the principle of inclusion-exclusion (PIE) to derive as simple as possible a formula for the number of derangements of a given finite set. Amazingly, it turns out that, as the number of elements goes to infinity, the fraction of permutations that are derangements approaches the reciprocal of Euler's constant e. Wow!
Like, subscribe, and share! To find out more about us:
- Reach out on Twitter at @ExistsforallA
Copyright © Existsforall Academy Inc. All rights reserved.
Like, subscribe, and share! To find out more about us:
- Reach out on Twitter at @ExistsforallA
Copyright © Existsforall Academy Inc. All rights reserved.
Counting Derangements in Combinatorics
[Discrete Mathematics] Derangements
Derangements - Numberphile
Derangements
(STa19) Permutations, Combinations, and Derangements
Arrangements and Derangements with Repetition
Derangement : Recursive relation proof (formula): Dn=(n-1)(Dn-1+Dn-2)
Permutations and Combinations Tutorial
Math 432: Permutations - Derangements (1 of 3)
Math 532 - 9.3: Derangements formula
Derangements of 4 numbers
Lecture 11 - DERANGEMENT permutation and combination// Combinatorics Discrete Math
Derangements recursive formula
Derangement || Combinatorics || ISI CMI Entrance || Math Olympiad
Derangements | Discrete Mathematics | Engineering Mathematics
COMBINATIONS with REPETITION - DISCRETE MATHEMATICS
Count Derangements | DP with Maths | Detailed solution with code | Love Babbar DSA sheet
Math 432: Permutations - Derangements (3 of 3)
Derangement ALL Standard Questions | Combinatorics Practice Set 3 Discussion | GO Classes | Deepak
Introduction to Circular Arrangements
How Do You Count Derangements?
Count Derangements | 4 Approaches | Dynamic Programming | Nagarro Summer internship
Introduction to Derangements
Derangement questions (Permutations and Combinations) Maths Extension 1 & 2 - PART 1
Комментарии
![[Discrete Mathematics] Derangements](https://i.ytimg.com/vi/BOFWLhH0Igo/hqdefault.jpg) 0:20:26
0:20:26
 0:08:33
0:08:33
 0:07:56
0:07:56
 0:32:30
0:32:30
 0:07:26
0:07:26
 0:06:09
0:06:09
 0:17:41
0:17:41
 0:07:03
0:07:03
 0:10:54
0:10:54
 0:01:56
0:01:56
 0:08:06
0:08:06
 0:20:04
0:20:04
 0:07:50
0:07:50
 0:17:44
0:17:44
 0:13:35
0:13:35
 0:20:37
0:20:37
 0:08:42
0:08:42
 2:27:48
2:27:48
 0:06:10
0:06:10
 0:09:02
0:09:02
 0:22:37
0:22:37
 0:03:05
0:03:05
 0:05:21
0:05:21