The Axiom of Choice | Epic Math Time

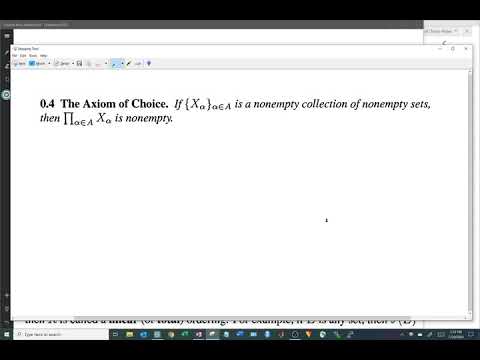
The axiom of choice states that the cartesian product of nonempty sets is nonempty. This doesn't sound controversial, and it might not even sound interesting, but adopting the axiom of choice has far reaching consequences in mathematics, and applying it in proofs has a very distinctive quality.

Special thanks to my Channel Supporters: Dru Vitale, RYAN KUEMPER, AlkanKondo89, John Patterson, Johann, Speedy, Zach Ager, Joseph Wofford, and Rainey Lyons.

My current equipment for making videos (affiliate links):

[EpicMathTime]

What are some other restrictions we could place on f, X, and Y, to guarantee a right inverse without needing the axiom of choice?

(Essentially, we need to impose enough "information" on those things for a choice function to be formed.)

[duncanw]

Skills they don't tell you you'll learn in math:

I can recognize a Springer-Verlag spine from a mile away.

[funkyflames]

I may not be super advanced in math, but math is what I want to study when I am older. And mathematicians like you provide in-depth explanations of super specific topics that make learning way easier when a textbook kinda fails. Even if I may not fully understand this yet, or I may not need to even be somewhat familiar, thanks a lot 😊

[captainsnake]

It still amazes you that you only have 20k subs. Your standard of quality is easily comparable to the biggest math channels, like 3b1b and Mathologer. By far the most underrated math channel.

[JamalAhmadMalik]

Just a videography tip here:
Wear something “contrastive.” Your T-shirt and heard blend with the background. You're basically a part of the wall. 😂
I love the quality tho.

[-sideddice]

I find your illustration of the logic link between the axiom of choice and the fact all sets are ordered most helpful !
We have 2 equivalent ways to get to the same conclusions !
Thanks for the video :)

[aquilazyy]

“Reach into the cosmos and grab” is a fantastic summarization of what the Axion of Choice does.

[NikolajKuntner]

Here's a nice AoC equivalent: Every infinity set A is in bijection with the product A x A. I personally don't think choice is something that should be added but I also consider it a bonus if your system is weak enough to just make it true. That said, you'll never convince the Zorn users to give it up. They build their gingerbread house a hundred years ago and it will keep being inherited until their lineage dies out.

[AndresFirte]

Dude I love your style, I didn’t understand everything in the video because I haven’t studied more about those topics, but it’s always nice to see your videos because of the way you present things, it’s super fun. And I think I learned the important aspects of what AC means, thanks :)

[charlesrockafellor]

AC (and ZFC, GCH, etc.): my favorite frenemy.

[MuffinsAPlenty]

This is a really nice video, especially how you go into the vibes of invoking the axiom.

[adeptusjoker]

Very good! I've never understood the AoC as well as this. Thank you

[jaydenmccutchen]

I saw your channel after reading a comment you left on Leo's channel, and love it.

[helixkirby]

What about Zorn's lemma? Might be cool to see a proof of the equivalence of the two

[juma]

How haven't I met your channel before? Amazing work

[alexanderthegreat]

best explanation I found on Youtube, good job

[haminatmiyaxwen]

Great video! = Graduate Texts in Background + Tool + Math

[mrluchtverfrisser]

I've got to say man, you keep surprising me with your quality. I was afraid this video might be slightly more sketchy/handwavey than usual, but you really make sure you know what you talk about and are not afraid to include it. Nice!

I'd share my own preferred take on including the axiom of choice, that I don't hear often:

It is not so much a limitation of ZF, that we need to include C. It is more so that we formulate ZF in first-order logic, which inherently describes finitistic reasoning. This is also why the finite version works fine: one just uses existential quantification elimination some finite number of times. But trying that same proof for infinite sets proofs impossible within first-order logic; but the mathematician wants to do so!

And here we should keep in mind logic has always had the role of giving an explenation about the reasoning of a mathematician. We logicians merely point out to the mathematicians that *if* they want to have this reasoning, and *if* they prefer a foundation in first order logic, *then* they are forced to inclide AoC. There is not necessarily a bad thing.

[ruinenlust_]

Actually a really nice explanation. Thank you!

[ahoj]

Interesting to note the following facts. Let A and B be two sets. If there is an injection from A to B and an injection from B to A, then there exists a bijection between A and B (Cantor-Bernstein theorem). The proof is not explicit, but does NOT require AC. But if you replace injection by surjection, then the conclusion is the same and does require AC. The axiom of choice also implies that, given two sets, there is alwyas an injection from one to the other (comparability of sets)