Chaos Game in a Hexagon

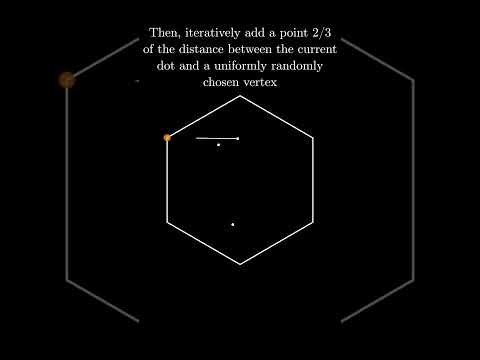
In this video, we explore the differences between starting with a random dot in a regular hexagon and iterating the procedure of choosing a hexagon vertex at random and moving either half the distance from the current dot to the chosen vertex OR two thirds the distance from the current dot to the chosen vertex. One of them leads to a stunning pattern (and has been color-coded for fun).

If you like this video, check out my others and consider subscribing. Thanks!

#chaos #chaosgame #hexagon #mathvideo​ #math​ #mtbos​ #manim​ #animation​ #theorem​​​ #iteachmath #mathematics #dynamicalsystems #iteratedfunctionsystem #dynamics #fractals

If you want to know more about the Chaos game, see the following links:

To learn more about animating with manim, check out:

_________________________________________
Music in this video:
Creative Commons Attribution-ShareAlike 3.0 Unported

[mathflipped]

These are really cool patterns that seem to appear out of random chaos.

[freshbakedclips]

"Rule(s) per say is not Random"

Chaos disappears the moment you apply Rules. Order emerges from the basic instruction of the game.

[MrUncivilrobot]

Could you do an MVP of Morley's trisector theorem? That seems like it was made for your format.

[rai]

i did this in excel, after watching a guy on tik tok talk about it. Very satisfying

[DrWeselcouch]

Wow what are the chances, I'm showing the Chaos Game to my Linear Algebra class tomorrow. I'm going to show them this video! :)

[alex_zetsu]

Wouldn't this be a fractal without chaos? If you had 2 different starting points and plotted them moving 2/3s to the same random vertex (that is the starting points are different but the sequence of vertexes are the same) wouldn't you end up with a similar pattern?

[spawn]

Can we do this for other shapes? I'd love to see it

[idorion]

Using an algorithm or set of rules is not fing chaos 🤦 it's very pre ordained by the very limited boundaries set

[MetaMaths]

Making snowflakes has never been harder