filmov
tv
Derivation of cosh and sinh

Показать описание
In this video, I derive the formulas for cosh and sinh from scratch, and show that they are indeed the hyperbolic versions of sin and cos. I also explain what the input x of cosh(x) means. Included is a calculation of the integral of sqrt(x^2-1)
Note: A big thanks to Alex Zorba, who came up with the idea and the proof, thank you 🙏
Note: A big thanks to Alex Zorba, who came up with the idea and the proof, thank you 🙏
Derivation of cosh and sinh
Hyperbolic Trig Functions - Basic Introduction
Hyperbolic Functions: Definitions, Identities, Derivatives, and Inverses
Why hyperbolic functions are actually really nice
Derivatives of Hyperbolic Functions
The applications of hyperbolic trig | Why do we even care about these things?
Definitions of Cosh and Sinh
Hyperbolic Trig Identities
Derivatives of all hyperbolic functions (proofs)
Hyperbolic Sine & Cosine
A-Level Further Maths H1-06 Hyperbolic Functions: Solve cosh(x)=3sinh(x)-1
Derivative of sinh(cosh(x)) #shorts
Hyperbolic Trig Functions THE HARD WAY
Introduction to Hyperbolic Trig Functions
A Perspective on sinh (x) & cosh (x) Definitions (hyperbolics)
sinh(x), cosh(x) and their derivatives + derivative of sinh(3x) and cosh differential equation.
Simple Derivation of sinh (x) and cosh (x) Integral Antiderivatives (via algebra)
Prove the identity cosh(x+y) = cosh x cosh y + sinh x sinh y. Hyperbolic functions
How to calculate Hyperbolic function sinh cosh using calculator
Hyperbolic Trigonometry Identity Proof: cosh(x+y) = cosh(x)cosh(y) + sinh(x)sinh(y)
Hyperbolic Trigonometric Identity: cosh(x-y)
Derivative of cosh (x^2+1) || Differentiation of Hyperbolic Trigonometric Functions
Derivative of cosh(x)
Derivatives of Inverse Hyperbolic Functions
Комментарии
 0:29:10
0:29:10
 0:10:12
0:10:12
 0:07:34
0:07:34
 0:16:03
0:16:03
 0:10:08
0:10:08
 0:14:45
0:14:45
 0:16:29
0:16:29
 0:11:46
0:11:46
 0:11:27
0:11:27
 0:05:35
0:05:35
 0:02:36
0:02:36
 0:00:38
0:00:38
 0:10:08
0:10:08
 0:08:21
0:08:21
 0:06:11
0:06:11
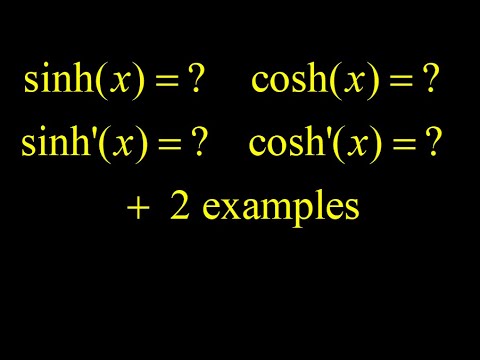 0:03:29
0:03:29
 0:04:34
0:04:34
 0:05:09
0:05:09
 0:00:49
0:00:49
 0:05:53
0:05:53
 0:04:02
0:04:02
 0:01:36
0:01:36
 0:03:19
0:03:19
 0:12:48
0:12:48