filmov
tv
Integral de dx entre 1 + sen x (Trigonométrica, multiplicando por conjugado)
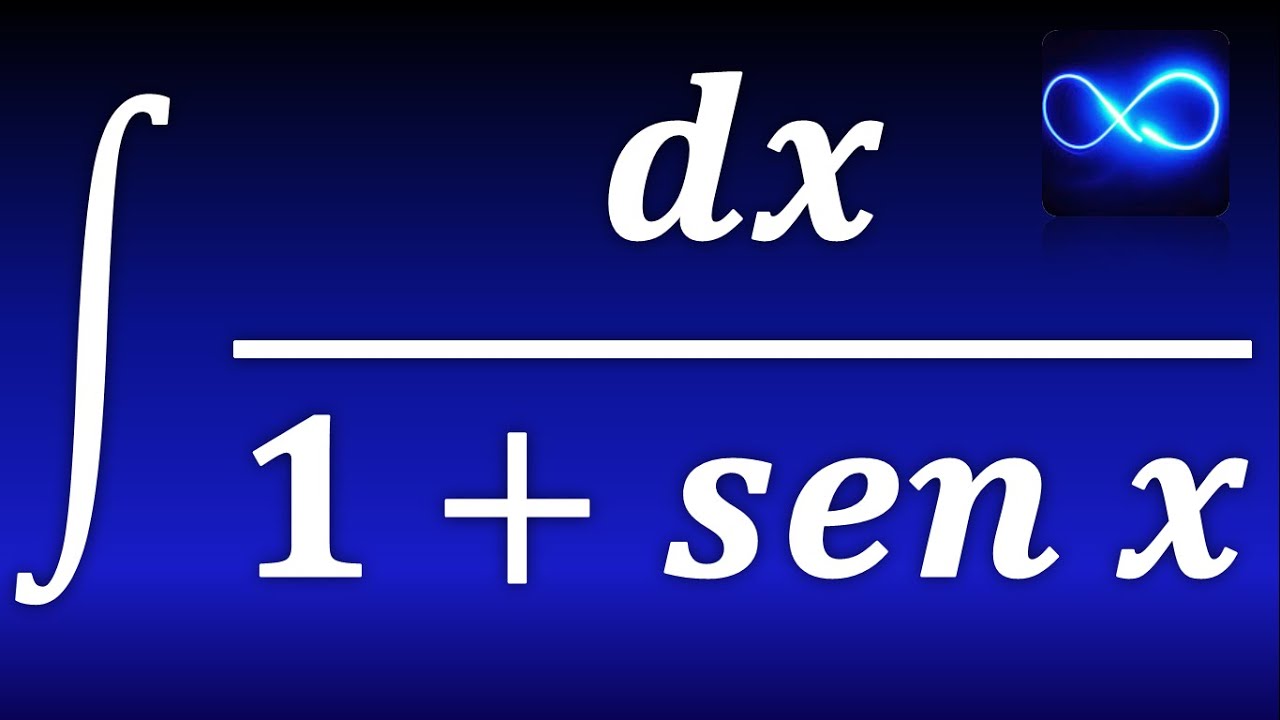
Показать описание
En este video resolveré una integral que contiene la forma 1 + sen x en el denominador, para ello multiplicamos por el conjugado y obtenemos así dos integrales trigonométricas muy sencillas, inmediatas.
#Integrales #Calculo #Integral
__________________________________
** ENLACES IMPORTANTES **
__________________________________
** MIRA TODOS MIS CURSOS AQUÍ **
__________________________________
** BIBLIOGRAFÍA **
- Cálculo de una variable, James Stewart
- Cálculo de una variable, Ron Larson
- Cálculo de una variable, Thomas
- Cálculo de una variable, Juan de Burgos
- Cálculo de una variable, Claudio Pita Ruiz
- Cálculo, Leithold
- Calculus, M. Spivak
- 5000 problemas de análisis matemático, B. Demidovich
- Calculus 1, Tom M. Apostol
- Matemáticas Simplificadas, de Conamat
__________________________________
** DONACIONES **
__________________________________
** MIS OTROS CANALES Y REDES SOCIALES **
__________________________________
#Matefacil #Matematicas #Math #tutorial #tutor #tutoriales #profesor
__________________________________
#Integrales #Calculo #Integral
__________________________________
** ENLACES IMPORTANTES **
__________________________________
** MIRA TODOS MIS CURSOS AQUÍ **
__________________________________
** BIBLIOGRAFÍA **
- Cálculo de una variable, James Stewart
- Cálculo de una variable, Ron Larson
- Cálculo de una variable, Thomas
- Cálculo de una variable, Juan de Burgos
- Cálculo de una variable, Claudio Pita Ruiz
- Cálculo, Leithold
- Calculus, M. Spivak
- 5000 problemas de análisis matemático, B. Demidovich
- Calculus 1, Tom M. Apostol
- Matemáticas Simplificadas, de Conamat
__________________________________
** DONACIONES **
__________________________________
** MIS OTROS CANALES Y REDES SOCIALES **
__________________________________
#Matefacil #Matematicas #Math #tutorial #tutor #tutoriales #profesor
__________________________________
Комментарии
 0:07:19
0:07:19
 0:07:58
0:07:58
 0:07:16
0:07:16
 0:03:19
0:03:19
 0:07:07
0:07:07
 0:03:43
0:03:43
 0:04:47
0:04:47
 0:00:54
0:00:54
 0:04:21
0:04:21
 0:02:16
0:02:16
 0:03:43
0:03:43
 0:53:10
0:53:10
 0:23:36
0:23:36
 0:02:40
0:02:40
 0:06:26
0:06:26
 0:05:12
0:05:12
 0:02:47
0:02:47
 0:08:48
0:08:48
 0:01:56
0:01:56
 0:02:30
0:02:30
 0:10:35
0:10:35
 0:13:09
0:13:09
 6:54:09
6:54:09
 0:03:46
0:03:46