Classification of left-invariant pseudo-Riemannian metrics on some nilpotent Lie groups (Yuji Kondo)

Yuji Kondo (Hiroshima University) - 9 March 2022

A classification of left-invariant pseudo-Riemannian metrics on some nilpotent Lie groups

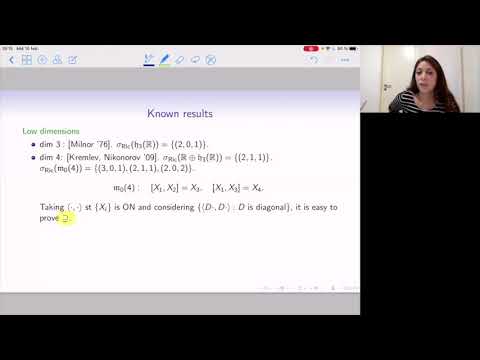
It is known that a connected and simply-connected Lie group admits only one left-invariant Riemannian metric up to scaling and isometry if and only if it is isomorphic to the Euclidean space, the Lie group of the real hyperbolic space, or the direct product of the three dimensional Heisenberg group and the Euclidean space of dimension n-3.

In this talk, I am going to talk about a classification of left-invariant pseudo-Riemannian metrics of an arbitrary signature for the third Lie groups with n greater than 3 up to scaling and automorphisms. This completes the classifications of left-invariant pseudo-Riemannian metrics for the above three Lie groups up to scaling and automorphisms.

Our classification can be obtained by a certain isometric action of cohomogeneity zero on a pseudo-Riemannian symmetric space. This action is not proper, in fact there exists a non-closed orbit, which allows us to consider degenerations of orbits. Finally, I explain that degenerations of orbits can have an implication with respect to curvature properties.

This study is based on the joint work with Hiroshi Tamaru from Osaka City University.