What is Zero Divided by Zero?

Learn what Zero divided by Zero really means.

Follow us on social media:
------------------------------------------
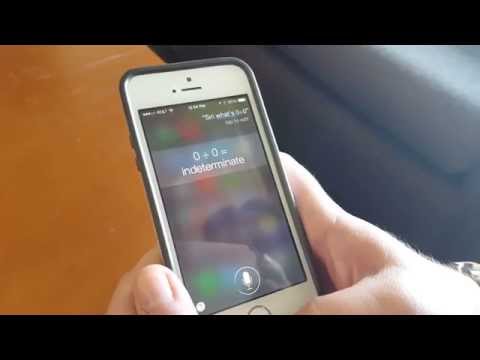
The short answer is that division by zero, whatever the dividend, is undefined in regular arithmetic. That is, this particular operation is not allowed by the rules of mathematics. People often take this to mean that the operation makes no sense physically, that the mathematics don’t model any sensical real-world situation. In the case of division by zero, this is a helpful visual. Division represents evenly splitting a certain number of objects (the dividend) into a certain number of groups (the divisor) and counting the number of objects in each resulting group (the quotient). The number of groups can be five, one million, or one, but it cannot be zero. Side note, people may argue that dividing some number of objects into zero groups is the same as not dividing it into groups, but that’s not true. Not dividing it into groups is the same as dividing it into one group, leaving the original group unchanged. This gives a good visual explanation of why dividing by zero makes no sense, but the truth is that a lot of things in math have no direct visual or physical representation and yet are useful in modelling the world around us. It’s better to think of an undefined operation as a banned rule breaker. Math is, at its core, a list of self-consistent rules, and if something breaks that self consistency, it must be thrown away.

The big rule that division by zero breaks is that, for a function to have an inverse, the function must be bijective. Let’s break that down. Normally, a function like “multiplication by 4” is undone by the function “division by 4”, and vice versa. So we say those two functions are inverses of each other. But this only works because multiplication by 4 is bijective, that is, for any number, if we multiply that number by 4, we get one and only one result. We can’t multiply a number by 4 and get two different answers, and we can’t multiply two different numbers by 4 and get the same result. To get the inverse function “division by 4”, we simply reverse these arrows. Multiplication by zero is different though. Any number multiplied by zero is zero, and no number can be multiplied by zero to give us a non-zero result. If we try to define the function “division by zero” by reversing these arrows, we have major problems. 0/0 has an infinite number of solutions, while any other number divided by zero has no solution. This is simply not a useful or sensical function, so it is not allowed. Multiplication by zero actually doesn’t break any mathematical rules for functions, it’s just not bijective. And it has a sensical physical representation to boot, since, for example, having three groups of no objects is a total of no objects. This is why multiplication by zero is allowed, but division by zero is simply not a thing.

We hope that gives you some deeper insight into why division by zero is undefined. If you have any questions or know of something we left out leave a comment below!

[MewtwoM]

This video makes perfect sense as to why it's not possible or even advisable to divide by zero, since it illustrates pretty much how I see the mere concept of attempting to divide by zero. The short answer is: It simply cannot be done. It would be like if you had a pizza and tried to split it with nobody. The end result would be a wasted pizza, since there would be nobody around to eat it, since there wouldn't be any slices, therefore the whole idea of trying to split a pizza with nobody would be pointless.

[saburousaitoh]

Please look our results:




on 2020-03-03 15:31:11, (98 unique-IP downloads)

Ankur Tiwari's Great Discovery of the Division by Zero $1/0 = \tan (\pi/2) = 0$ on $ 2011$

Authors: Saburou Saitoh,  Yoshinori Saitoh
Category: Functions and Analysis

on 2020-02-19 16:03:00, (90 unique-IP downloads)

Division by Zero Calculus For Differentiable Functions in Multiply Dimensions

Authors: Saburou Saitoh
Category: Functions and Analysis

on 2020-01-27 16:28:38, (49 unique-IP downloads)

Division by Zero Calculus, Derivatives and Laurent's Expansion

Authors: Saburou Saitoh
Category: Functions and Analysis

on 2020-01-06 17:52:07, (58 unique-IP downloads)

Division by Zero Calculus for Differentiable Functions L'Hôpital's Theorem Versions

Authors: Saburou Saitoh
Category: Functions and Analysis

on 2019-12-16 18:37:53, (94 unique-IP downloads)

Essential Problems on the Origins of Mathematics; Division by Zero Calculus and New World

Authors: Saburou Saitoh
Category: Functions and Analysis

[chaosvolt]

HOLD UP. "And we can't multiply two different numbers by four and get the same result."

Doesn't that make multiplication by zero invalid as well, due to every number multiplied by zero equaling zero? It makes it feel like dealing with zero like this already breaches bijectivity. This is a big problem because "remember that multiplying any number by zero makes zero" is always upheld as the root for why "zero divided by zero" is considered unacceptable, despite being arguably correct.

If one times zero equals zero, but zero divided by zero does not equal one, then that means that allowing any number to be multiplied by zero runs afoul of this rule, and it runs afoul of the issue that we can reach zero using any multiplier this way. This means that accepting multiplication by zero as valid, despite being impossible to correctly invert AND allowing wildly different equations, is already a breach of mathematical principles.

Using multiplication by zero, which is in breach of these principles, to prove that "0 / = 0" is invalid due to being in breach of said principles, is thus completely disingenuous.

[saburousaitoh]

0/0=0 was known about 1300 years ago in India; now 0/0=1/0= tan(\pi/2)=0. However you have to find their definitions and meanings: viXra:1908.0100 submitted on 2019-08-06 20:03:01, (709 unique-IP downloads)

Fundamental of Mathematics; Division by Zero Calculus and a New Axiom