No more confusion on square root

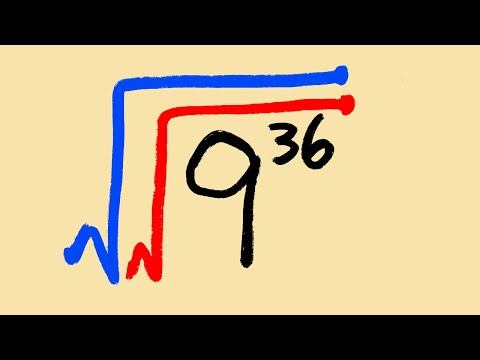
We will talk about why the square root (when you use the square root symbol) of 36 is just 6. We will also talk about the common mistake that people get mixed up between evaluating sqrt(36) and solving x^2=36. Subscribe to @bprpmathbasics for more math basics that you need for your algebra class!

-----------------------------
-----------------------------
#math #algebra #mathbasics

[evank]

If the question gives you the sqrt, it’s positive. If you create the sqrt, it’s plus or minus

[altarius]

another way to understand it is through functions: for f(x) = x², there are two possible x-values that give 16 (namely 4 and -4). However, if g(x) = √x and you evaluate g(16) it's only 4 because a function assigns no more than one value to each x. (You plug in 16 and you get the definite result 4, not a 50% chance of 4 and a 50% chance of -4)

[DerangedIntellectual]

THANK YOU FOR MAKING THIS AND CLEARING UP THE CONFUSION (I'm a sophomore university engineering student and I'm ashamed to admit I was still confused about this at times because I wish I had it all on memory without having to think about it when asked... until I watched this vid. So thank you!)

[owlsmath]

Awesome! Great way to cover all cases (in about 40 seconds!)

[celestialTangle]

(5, 12, 13) is the Waluigi of pythagorean triples

[luuminhhuy]

In Vietnam we were taught to just put the plus or minus symbol before the square root symbol to differentiate between the two possible values of the square root. Slightly confusing but convenient, I guess
Edit: Here I meant a square root with a plus symbol (normally omitted), and another one with a negative sign, not putting the ± sign before the square root, basically the way that @Russel Thorburn suggested

[crazytiger]

I learned that when evaluating the square root symbol that you only add the plus or minus symbol if you added the square root symbol yourself, if it was already part of the equation, just positive

[anuragmahajan]

Thank you very much! I have been always confused about this

[Ninja]

What i find so ironic about this topic is that people always say like sqrt(4) = +/- 2 for example, but no one ever says like
sqrt(2) = +/- 1.4142… or sqrt of any other non perfect square.

All things aside, i do feel the confusion comes w scenario 1 and 3, especially when we talk about complex numbers. In real numbers radicals are single-valued but in complex numbers they are multi-valued

[doggo]

Once I've heard square roots are an absolute value, hence why its always positive. So when we do "sqrt(x²)", the answer is "|x|". But as we usually want to find the value of x, it can be both positive and negative.
As in the example, sqrt(36) = |+6| and |-6|, both result in 6, and x = +/- 6

Idk if it is correct to say, but it does make sense to me
edit: spelling

[turtlemaster-gzdc]

my teacher always taught me "if you put YOUR OWN radical in the equation, like you did in problem 2, then use +/-, but if it was already there, like in problem 1, then don't worry"

[jaysonkmendoza]

Yup. Makes sense because if you had two outcomes then the output is not function because functions map a single input to a single output by definition.

However it’s important to know what your trying to find because people use the functional notation when they are trying to solve.

The most common reason for dual answers is factoring.

[Steve_Stowers]

I think a lot of the confusion comes in because, even though the square root symbol (radical sign) denotes the PRINCIPAL square root, many of us get lazy and read it as "the square root." (I'm guilty of this myself.) For example, we read √2 as "the square root of 2, " assuming everyone knows we really mean the principal (i.e. positive) square root of 2.

[TheTransforcer]

That staring the camera down during the last example was such a flex.

[tehguitarque]

I've never had this confusion or frankly come across it and therefore was confused by this!

[DorianC]

I never knew this but very helpful! Thank you!

[tontonbeber]

And you can go even further ... with cubic root ... So cubic root as a function is defined such a way that cubic root of -1 is -1.
But this is not equivalent of the power operation defined on complex numbers.
It you evaluate the result of (-1)^(1/3), it is NOT -1 but the first root of -1, i.e. (1/2)+i(V3/2)

[Zasil]

I remember from school that sqrt(x^2)=|x|. No more confusion after that...

[ghostwarrior]

How about making a compilation of you just banging your pen against the board? idk why i find it so satisfying

[iharshbrown]

Simplest way to understand this:
For x^2=36,
x=+√36 or -√36
x=6 or -6

However, if the question just states "Find √36", then the answer is only 6
In contrast, if the question states "Find -√36", then the answer is only -6