filmov
tv
Clear Explanation of Zeros and Non-Minimum Phase Zeros of Transfer Functions and Effect on Dynamics
Показать описание
#controltheory #mechatronics #systemidentification #machinelearning #datascience #recurrentneuralnetworks #signalprocessing #dynamics #mechanics #mechanicalengineering #controltheory #mechatronics #robotics #astrodynamics #astrophysics #physics #chaos #mathematics #mathematicians#electricalengineering #mechanicalengineering #engineering #leastsquares #nonlinearsystems #modelpredictivecontrol #optimalcontrol #controlengineering #controltheory #optimalcontrol #modelpredictivecontrol #robotics #reinforcementlearning #automation #industrialautomation #processcontrol #systemidentification #machinelearning #python #optimization #datascience #timeseries #automation #robotics #mechatronics #gnc #nonlinear #mathematics #signalprocessing #processengineering #processautomation
It takes a significant amount of time and energy to create these free video tutorials. You can support my efforts in this way:
- You Can also press the Thanks YouTube Dollar button
The webpage accompanying this video tutorial is given here:
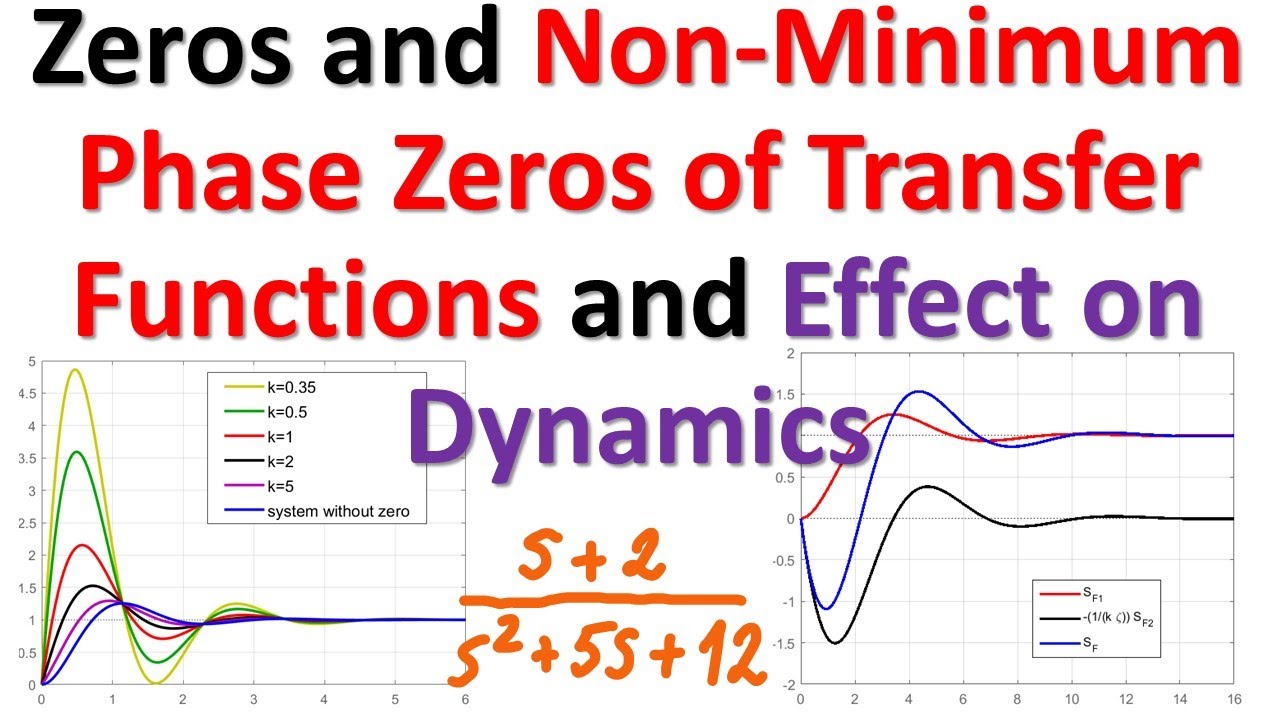
In this control engineering tutorial, we will explain the effect of zeros of transfer functions on the dynamical behavior of systems. This important topic is often overlooked or not properly explained in the control engineering courses. The general impression that we have is that students often do not understand the zeros of transfer functions and their effects on the dynamical system behavior and response. Zeros play a very important role in control system analysis and design. If their effect is not properly understood, one will never be able to design a high-performance control system.
Here is a brief outline of what you will learn in this video tutorial. First, we will show that if a zero is close to a pole of the transfer function then the corresponding influence of the pole on the dynamical system response will be decreased. Then, we will show that if zeros are close to the real parts of the poles and to the imaginary axis, then their effect is to increase the system overshoot. We then mathematically explain that the zeros actually introduce derivative actions in the step response, that is, they amplify the response. On the other hand, we also analyze the effect of non-minimum phase zeros. Non-minimum phase zeros are zeros with positive real parts. We show that the non-minimum phase zeros introduce a negative overshoot in the system response which can have a devastating effect on the system response.
It takes a significant amount of time and energy to create these free video tutorials. You can support my efforts in this way:
- You Can also press the Thanks YouTube Dollar button
The webpage accompanying this video tutorial is given here:
In this control engineering tutorial, we will explain the effect of zeros of transfer functions on the dynamical behavior of systems. This important topic is often overlooked or not properly explained in the control engineering courses. The general impression that we have is that students often do not understand the zeros of transfer functions and their effects on the dynamical system behavior and response. Zeros play a very important role in control system analysis and design. If their effect is not properly understood, one will never be able to design a high-performance control system.
Here is a brief outline of what you will learn in this video tutorial. First, we will show that if a zero is close to a pole of the transfer function then the corresponding influence of the pole on the dynamical system response will be decreased. Then, we will show that if zeros are close to the real parts of the poles and to the imaginary axis, then their effect is to increase the system overshoot. We then mathematically explain that the zeros actually introduce derivative actions in the step response, that is, they amplify the response. On the other hand, we also analyze the effect of non-minimum phase zeros. Non-minimum phase zeros are zeros with positive real parts. We show that the non-minimum phase zeros introduce a negative overshoot in the system response which can have a devastating effect on the system response.
Комментарии
 0:12:18
0:12:18
 0:06:39
0:06:39
 0:05:09
0:05:09
 0:05:48
0:05:48
 0:03:43
0:03:43
 0:05:30
0:05:30
 0:04:30
0:04:30
 0:00:54
0:00:54
 0:10:04
0:10:04
 0:02:15
0:02:15
 0:04:51
0:04:51
 0:01:55
0:01:55
 0:07:17
0:07:17
 0:15:52
0:15:52
 0:00:54
0:00:54
 0:00:19
0:00:19
 0:06:20
0:06:20
 0:02:43
0:02:43
 0:08:56
0:08:56
 0:02:04
0:02:04
 0:00:44
0:00:44
 0:00:30
0:00:30
 0:24:24
0:24:24
 0:00:32
0:00:32