filmov
tv
Proving a Quick and Easy Inequality (1+1/x)(1+1/y)≥9
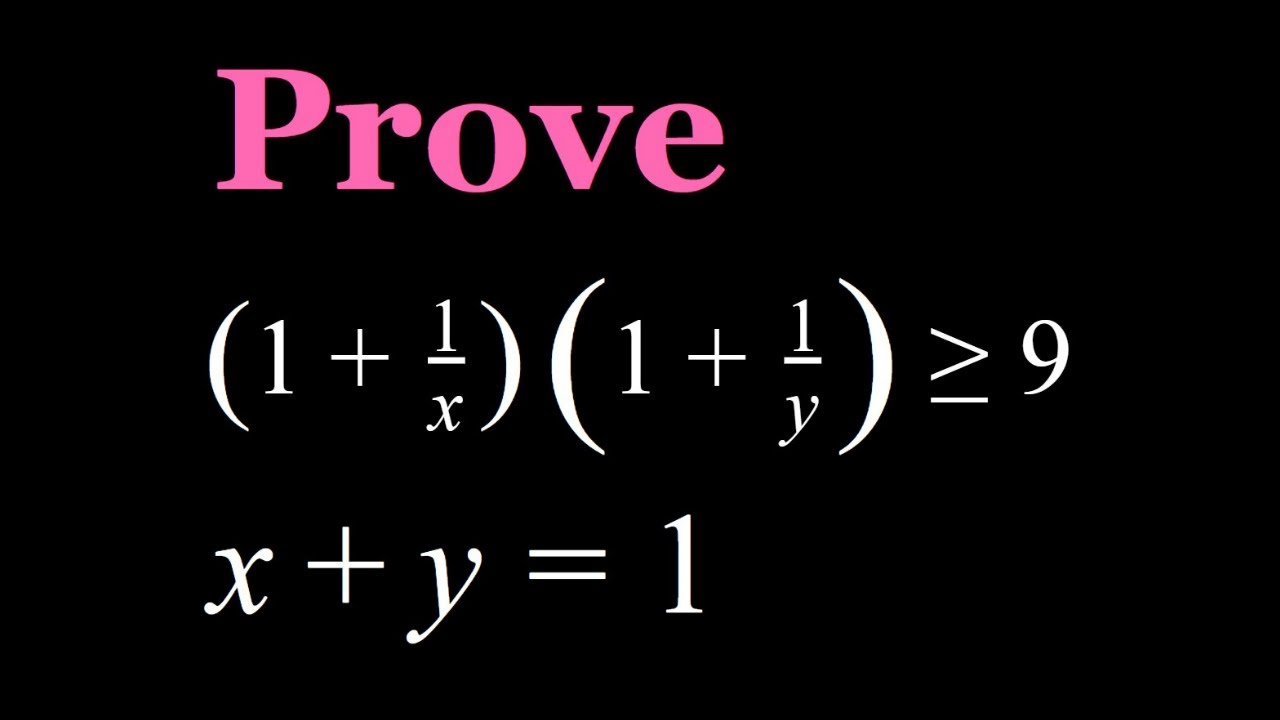
Показать описание
If you need to post a picture of your solution or idea:
#ChallengingMathProblems #ProvingInequalities
EXPLORE 😎:
PLAYLISTS 🎵 :
#ChallengingMathProblems #ProvingInequalities
EXPLORE 😎:
PLAYLISTS 🎵 :
Proving a Quick and Easy Inequality
Proving a Quick and Easy Inequality
Proving a Quick and Easy Inequality
Proving a Quick and Easy Inequality (1+1/x)(1+1/y)≥9
He PROVED That LOSING WEIGHT Is EASY (@azovsky__dm)
Proving a quick easy inequality #shorts
Proof that Mandarin Chinese is Easy
easy to state -- hard to prove
BLACKOUT PROOF Your Home in Just 7 Days with These Simple Steps
How To EASILY Prove God To An Atheist
Proof Men Are Simple.!🙂#trollface #hkqedits
A Simple and Beautiful proof of The Fundamental Theorem of Algebra
Proof Made Easy | Maths GCSE
Proving Similar Triangles Made EASY | Maths GCSE
Simple Proof of the Pythagorean Theorem
Simple Pythagorean Dissection Proof
THIS Is Why That Simple Three Step Rule Can Prove Useful | Jordan Peterson #shorts
Day #1 of proving that the piano is simple 💪 #piano #tutorial #pianolessons
π is Irrational: A Simple Proof 🥧
Cute easy hairstyles for medium, long hair 😍✨ #hairstyles #hairtok #hair #shorts #explorepage
A simple yet effective life hack that could prove invaluable in an emergency. #shorts
Fast, Easy, Secure Digital Onboarding with Prove Pre-fill
Apple phone personalized Z case, simple and drop-proof, restores the feel of the bare phone #shorts
Easy fail-proof apple crisp that’s perfect for fall baking! | FeelGoodFoodie
Комментарии
 0:08:58
0:08:58
 0:05:38
0:05:38
 0:05:38
0:05:38
 0:08:58
0:08:58
 0:00:33
0:00:33
 0:00:32
0:00:32
 0:00:19
0:00:19
 0:00:41
0:00:41
 1:24:19
1:24:19
 0:09:35
0:09:35
 0:00:13
0:00:13
 0:01:28
0:01:28
 0:01:00
0:01:00
 0:00:59
0:00:59
 0:03:40
0:03:40
 0:00:59
0:00:59
 0:00:58
0:00:58
 0:00:19
0:00:19
 0:08:47
0:08:47
 0:00:11
0:00:11
 0:00:17
0:00:17
 0:01:05
0:01:05
 0:00:18
0:00:18
 0:00:25
0:00:25