filmov
tv
Ex 3B Q31 to Q40 Class 10 Linear Equations in two Variables RS Aggarwal CBSE | New Syllabus
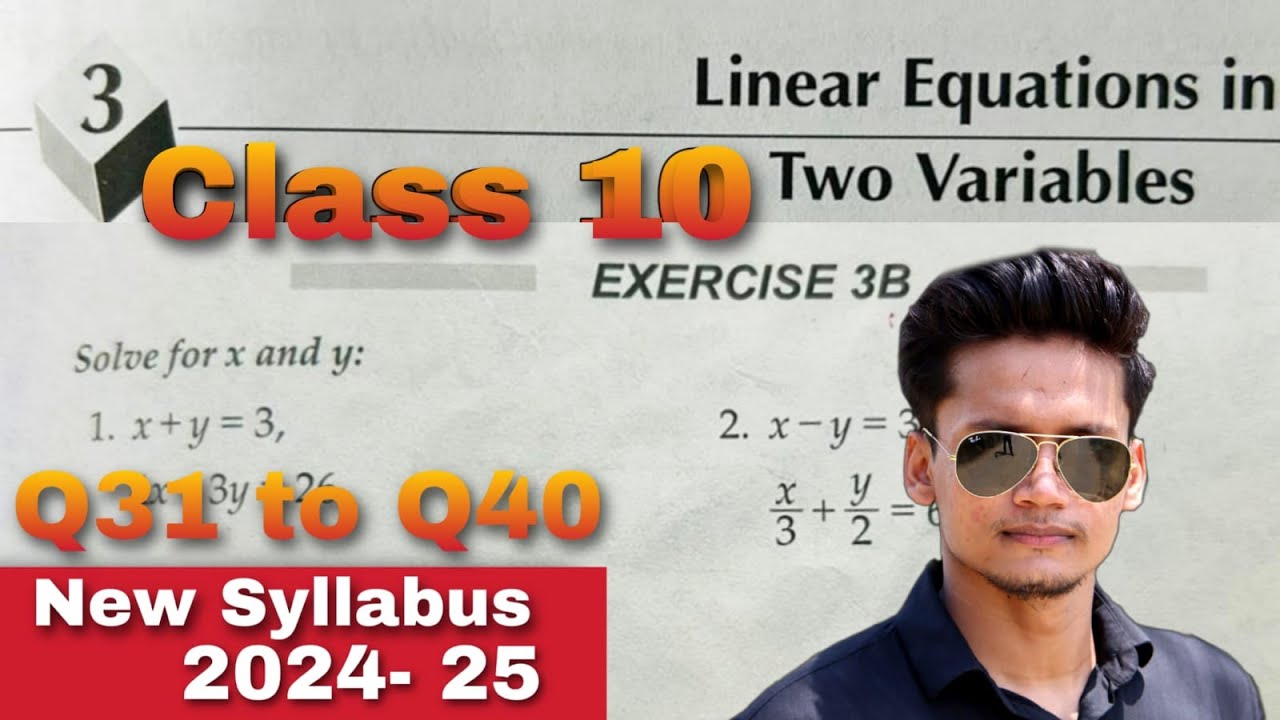
Показать описание
Book - RS Aggarwal
Book - NCERT
Class - 10
Chapter -Linear Equations in two Variables
exercise 3B
Q31 to Q40
``````````````````````````
exercise 3B
Q41 to Q51
- - - - - - - - - - - - - - - - - - - - - - - - - - - - -
BE MY FRIEND :-----
- - - - - - - - - - - - - - -- - - - - -- - - - - - - - - - - -
ex 3b q31 ex 3b class10 rs aggrwal rs aggarwal class 10 chapter 10 ex 3b rs aggrwal ex 3b q40
An equation is said to be linear equation in two variables if it is written in the form of ax + by + c=0, where a, b & c are real numbers and the coefficients of x and y, i.e a and b respectively, are not equal to zero.
For example, 10x+4y = 3 and -x+5y = 2 are linear equations in two variables.
The solution for such an equation is a pair of values, one for x and one for y which further makes the two sides of an equation equal.
The solution of linear equations in two variables, ax+by = c, is a particular point in the graph, such that when x-coordinate is multiplied by a and y-coordinate is multiplied by b, then the sum of these two values will be equal to c.
Basically, for linear equation in two variables, there are infinitely many solutions.
Example
In order to find the solution of Linear equation in 2 variables, two equations should be known to us.
Consider for Example:
5x + 3y = 30
The above equation has two variables namely x and y.
Graphically this equation can be represented by substituting the variables to zero.
linear equations in two variables class 10 class 1 0 linear equations in two variables maths chapter 3 class 10 ex 3b class10 rs aggrwal rs aggarwal class 10 chapter 10 ex 3b Q21 to q20 class 10 ex 3b q21 class 10 ex 3b q30 EX 3B q11 RS AGGARWAL CLASS 10 Exercise 3B Q30 class 10 ex 3b rs aggrwal,ex 3b Q1 dear ir,;earn maths shobhit nirwan,Class 10 ex 3B Q21 Q30 ex 3B class 10 ex 3b Q11to Q19 rs aggarwal,rs aggarwal class 10 ex 3b rs aggarwal
Book - NCERT
Class - 10
Chapter -Linear Equations in two Variables
exercise 3B
Q31 to Q40
``````````````````````````
exercise 3B
Q41 to Q51
- - - - - - - - - - - - - - - - - - - - - - - - - - - - -
BE MY FRIEND :-----
- - - - - - - - - - - - - - -- - - - - -- - - - - - - - - - - -
ex 3b q31 ex 3b class10 rs aggrwal rs aggarwal class 10 chapter 10 ex 3b rs aggrwal ex 3b q40
An equation is said to be linear equation in two variables if it is written in the form of ax + by + c=0, where a, b & c are real numbers and the coefficients of x and y, i.e a and b respectively, are not equal to zero.
For example, 10x+4y = 3 and -x+5y = 2 are linear equations in two variables.
The solution for such an equation is a pair of values, one for x and one for y which further makes the two sides of an equation equal.
The solution of linear equations in two variables, ax+by = c, is a particular point in the graph, such that when x-coordinate is multiplied by a and y-coordinate is multiplied by b, then the sum of these two values will be equal to c.
Basically, for linear equation in two variables, there are infinitely many solutions.
Example
In order to find the solution of Linear equation in 2 variables, two equations should be known to us.
Consider for Example:
5x + 3y = 30
The above equation has two variables namely x and y.
Graphically this equation can be represented by substituting the variables to zero.
linear equations in two variables class 10 class 1 0 linear equations in two variables maths chapter 3 class 10 ex 3b class10 rs aggrwal rs aggarwal class 10 chapter 10 ex 3b Q21 to q20 class 10 ex 3b q21 class 10 ex 3b q30 EX 3B q11 RS AGGARWAL CLASS 10 Exercise 3B Q30 class 10 ex 3b rs aggrwal,ex 3b Q1 dear ir,;earn maths shobhit nirwan,Class 10 ex 3B Q21 Q30 ex 3B class 10 ex 3b Q11to Q19 rs aggarwal,rs aggarwal class 10 ex 3b rs aggarwal
Комментарии
 0:55:54
0:55:54
 0:16:38
0:16:38
 0:14:45
0:14:45
 0:54:19
0:54:19
 0:53:39
0:53:39
 0:23:18
0:23:18
 0:14:15
0:14:15
 0:04:12
0:04:12
 0:35:54
0:35:54
 0:15:42
0:15:42
 0:00:46
0:00:46
 0:15:28
0:15:28
 0:05:08
0:05:08
 0:02:40
0:02:40
 0:13:21
0:13:21
 0:00:47
0:00:47
 0:00:58
0:00:58
 0:01:27
0:01:27
 0:05:42
0:05:42
 0:00:56
0:00:56
 0:04:54
0:04:54
 0:29:05
0:29:05
 0:48:36
0:48:36
 0:01:00
0:01:00