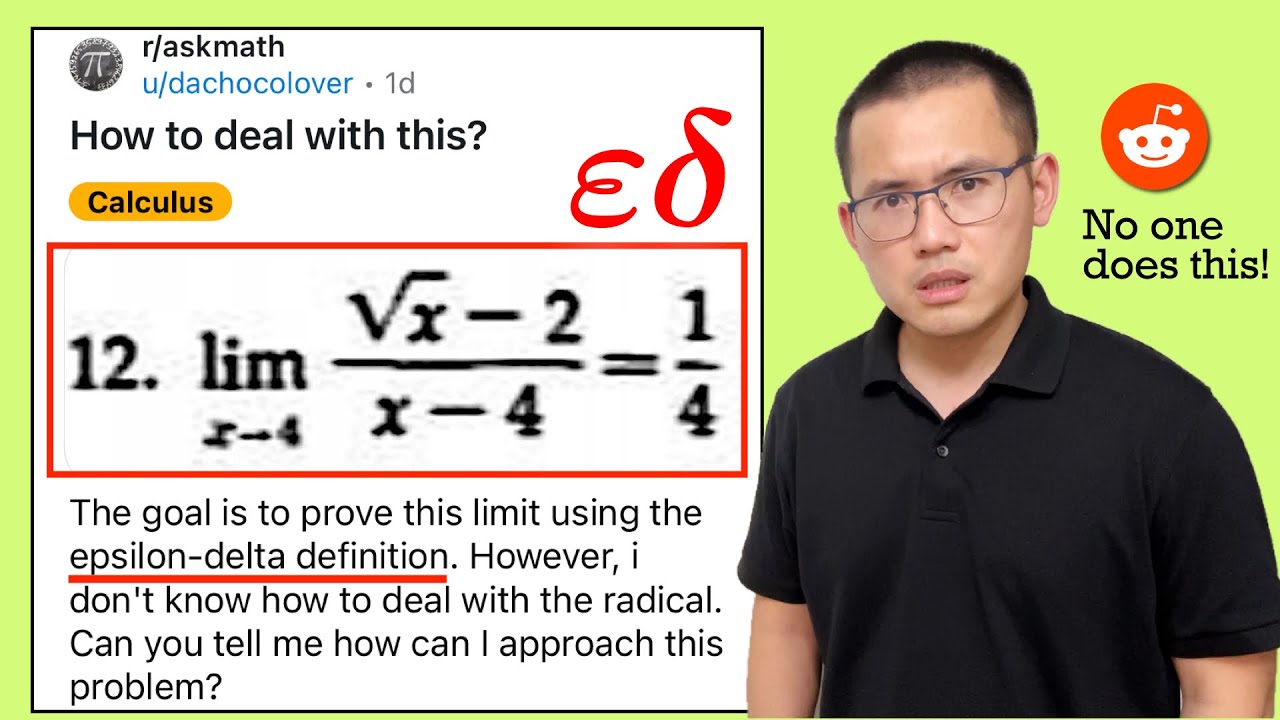
No one proves this kinda limit with the epsilon-delta definition! Reddit r/askmath

-----------------------------
Support this channel and get my calculus notes on Patreon: 👉
-----------------------------
#calculus #bprpcalculus #apcalculus #tutorial #math

[zachedwards]

Notice you can make the second side of the proof slightly quicker. First, before you get rid of the 4(sqrt(x)+2) in the denominator you can quickly rewrite abs(-sqrt(x)+2 ) as abs(sqrt(x)-2) like you do later since absolute value is an even function (i.e. abs(x)=abs(-x)). Then you can multiply by the conjugate before you get rid of that denominator. Then the top becomes abs(x-4) and the bottom becomes 4(sqrt(x)+2)^2, which is still greater than 1, so we can say that the ratio is less than abs(x-4), which is then less than δ, which we set equal to ε. Notice that doing the conjugate step before getting rid of 4(sqrt(x) +2) in the denominator helps us not have to do the step of getting rid of the denominator twice like you had to do in your version. Hope this helps. Great video.

[kingbeauregard]

I find that, to understand epsilon-delta, imagine a rectangle centered at (a, L) that is tall / narrow enough that your function f(x) doesn't touch the top or bottom edge. Now, can you shrink that rectangle down to nothing, without f(x) touching the top or bottom edges at any time? You can change the shape of the rectangle as you go, just as long as the height and width reach 0 at the same time.

Anyway, if you can do rectangles that work like that, the limit exists. To put it differently, the limit exists if, the closer you get to your point vertically, the closer you also get horizontally. And all this epsilon-delta jazz is about proving that you can make these rectangles: if you can work out dimensions of rectangles that work like this, then the limit must exist.

That's WHY epsilon-delta works.

Now HOW it works is another matter. What you want to do with f(x) is try to turn it into (x-a)*(everything else). You have two tricks you can use:

1) You can replace f(x) with a slightly different function that you know is always "bigger" than f(x), and then do epsilon-delta on that function. If epsilon-delta proves the limit on g(x), and g(x) is always "bigger" than f(x), then squeeze proof logic says that f(x) must have the same limit.

2) You can limit your domain to a narrow region around (a, L). A good idea is to try to go narrow enough to avoid any extrema and singularities. Failing that - if it really really doesn't matter how narrow your region is - just use a value of 1.

[fizisistguy]

Idk about this concept, but factorization did this in 5 seconds

[MasterHigure]

I didn't grok epsilon-delta until I got to real analysis. My book drew an arbitrary function as a diagram with domain and codomain entirely separate and a function being a collection of arrows from one to the other. Parsing out what epsilon-delta means in terms of such a diagram is what actually made it click for me.

Trying to parse out epsilon-delta in a standard function graph results in a cluttered mess that didn't teach me anything.

[IOSARBX]

bprp calculus basics, cool video I really liked it

[jarikosonen]

10:48 How is this abs(sqrt(x)-2)*(sqrt(x)+2) calculated?
Is it really abs(x-4)?

[josephgyasiborr]

Pls sir I still don't understand, is it that we just throw away the denominator?? Pls explain

[DotRabbit]

Lim x→4 (x½-2)'/(x-4)' = lim x→4 1/(2√x) = 1/(2(2)) = 1/4

[zyklos]

Hated that e-d "tool" of math, since it introduced unequalities, absolute values and strange behaving limits, which comes very unhandy right after you start trying.
But it's justified reasoning so that you can reduce error to your goal by finding a function e(d) to choose d from. But you never reach your goal. Disappointing 😂
Now I have to think, can't you rewirte the problem as
| (sqrt(x-d) - 2) / (x - d - 4) - 1/4 | < e
Then somehow bring it along

[drazenbicanic]

Why the complication. divide x-4 into the difference of squares (sqrtx+2)(sqrtx-2), shorten the numerator (sqrtx-2) with part of the denominator, and it remains 1/(sqrtx+2). Let's add 4 and get 1/4

[DrRBERT]

If this was for a first semester intro to analysis course, I would be fine with the question. But, as someone who has taught 𝛆-𝛅 proofs in calculus courses at university and at a community college, the topic goes over like a lead balloon. The students don't get it, and it ends up being how to tweak previous problems' algebra to get the result without really understanding what's going on. It effectively wastes so much time. I no longer cover the proofs. I instead spend half an hour to discuss what the geometric interpretations of 𝛆-𝛅 proofs. What helps with the understanding is showing graphs where the limit does not exist in the 𝛆-𝛅 context. They get the concept much better. I move on.