filmov
tv
Divide Monomials the Easy Way

Показать описание
Alright, picture this: you've just walked into the coolest party ever, but instead of DJs and dance floors, it's all about dividing monomials, which, believe it or not, can be just as thrilling once you get the hang of it. So, what's a monomial? Imagine it as a solo artist in the vast music world of algebra, a single term consisting of numbers and variables mashed together through multiplication.
Now, diving into dividing monomials is like mastering the art of sharing your favorite giant pizza evenly among friends. The key ingredients? Numbers, variables, and a sprinkle of exponents. Here’s the secret recipe: When you divide monomials, you're basically slicing up the pizza so everyone gets an equal share. But instead of pizza, we're sharing numbers and variables.
First up, tackle the numbers like you’d split a bill - just divide them. Easy, right? Next, move on to the variables (those letters that seem random but actually hold the universe’s secrets). Dividing variables is like dealing with leftovers - you subtract the exponent (or power) of the variable in the denominator from the exponent in the numerator. So, if you have \(x^5\) divided by \(x^2\), you simply subtract the exponents: 5 - 2 = 3, leaving you with \(x^3\).
What if the exponents are the same, like \(x^3\) divided by \(x^3\)? They cancel each other out, leaving you with a cool, crisp 1. It's like having an equal number of slices for everyone, so no one's left hungry (or mathematically unsatisfied).
And there you have it, dividing monomials is just a way of sharing and simplifying, turning complex algebraic expressions into something more manageable, like turning a whole pizza into satisfying slices. So, next time you're faced with a division of monomials, remember, it's all about sharing the algebraic love evenly.
Now, diving into dividing monomials is like mastering the art of sharing your favorite giant pizza evenly among friends. The key ingredients? Numbers, variables, and a sprinkle of exponents. Here’s the secret recipe: When you divide monomials, you're basically slicing up the pizza so everyone gets an equal share. But instead of pizza, we're sharing numbers and variables.
First up, tackle the numbers like you’d split a bill - just divide them. Easy, right? Next, move on to the variables (those letters that seem random but actually hold the universe’s secrets). Dividing variables is like dealing with leftovers - you subtract the exponent (or power) of the variable in the denominator from the exponent in the numerator. So, if you have \(x^5\) divided by \(x^2\), you simply subtract the exponents: 5 - 2 = 3, leaving you with \(x^3\).
What if the exponents are the same, like \(x^3\) divided by \(x^3\)? They cancel each other out, leaving you with a cool, crisp 1. It's like having an equal number of slices for everyone, so no one's left hungry (or mathematically unsatisfied).
And there you have it, dividing monomials is just a way of sharing and simplifying, turning complex algebraic expressions into something more manageable, like turning a whole pizza into satisfying slices. So, next time you're faced with a division of monomials, remember, it's all about sharing the algebraic love evenly.
 0:06:53
0:06:53
 0:00:56
0:00:56
 0:03:04
0:03:04
 0:02:00
0:02:00
 0:12:43
0:12:43
 0:10:49
0:10:49
 0:00:55
0:00:55
 0:00:57
0:00:57
 0:01:00
0:01:00
 0:00:56
0:00:56
 0:02:09
0:02:09
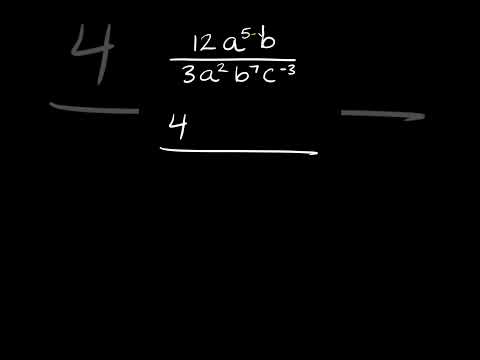 0:01:00
0:01:00
 0:00:59
0:00:59
 0:00:23
0:00:23
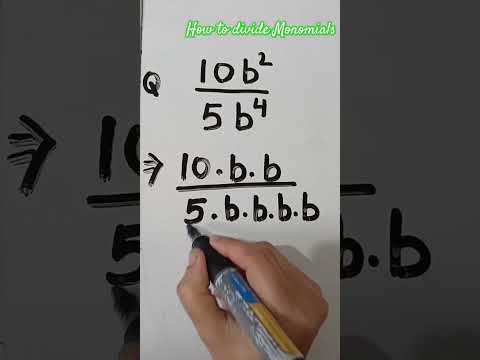 0:00:26
0:00:26
 0:06:03
0:06:03
 0:12:12
0:12:12
 0:00:15
0:00:15
 0:00:18
0:00:18
 0:00:16
0:00:16
 0:13:35
0:13:35
 0:13:56
0:13:56
 0:01:01
0:01:01
 0:13:34
0:13:34