Exponential Population Growth Equation w/ 2 Points. f(x)=ab^x. 'Exponential Regression'

preview_player
Показать описание
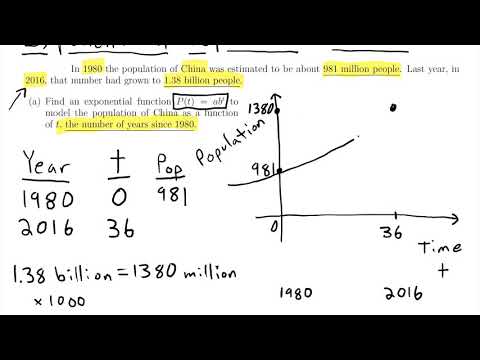
This is an example problem using the population of China in 1980 and 2016 to create an exponential function of the form P(t) = ab^t and then use that function to predict the population in 2030.

Notes:
t = the number of years since 1980
P(t) = the population of China in millions

If you have a ti-84 you can determine the values of "a" and "b" in the P(t) = ab^t by inputting the points (0,981) and (36, 1380) into L1 and L2 ("stat" , edit) and then ("stat" , calc , 0:ExpReg ).
  1. Sulock Math
  2. algebra
  3. exponential growth
  4. exponential regression
  5. exponential model
  6. f(t) = ab^t
Рекомендации по теме
Exponential Population Growth 0:05:25

Exponential Population Growth Equation w/ 2 Points. f(x)=ab^x. 'Exponential Regression'

Exponential Population Growth 0:04:55

Exponential Population Growth

Exponential Growth and 0:13:02

Exponential Growth and Decay Calculus, Relative Growth Rate, Differential Equations, Word Problems

Exponential Population Growth 0:11:57

Exponential Population Growth Model

Exponential Logistic Growth 0:05:52

Exponential Logistic Growth AP Biology

How to Use 0:08:03

How to Use Population Growth Models Ft. The Math Sorcerer

Population Growth Models 0:08:52

Population Growth Models [Exponential & Logistic Growth]

Exponential Growth 0:10:09

Exponential Growth

Algebra - Solving 0:02:30

Algebra - Solving Exponential Equation Example 1 #math #algebra

Exponential and logistic 0:07:32

Exponential and logistic growth in populations | High school biology | Khan Academy

Ecology- Population Exponential 0:05:11

Ecology- Population Exponential Growth Equation

[20.0] Exponential Growth 0:07:59

[20.0] Exponential Growth and Decay: Population of Protozoa with Constant Growth

Ex: Exponential Growth 0:07:46

Ex: Exponential Growth Function - Population

Exponential Population Growth 0:13:02

Exponential Population Growth Model (Derivation & Application)

Write an Exponential 0:03:03

Write an Exponential Equation to Model World Population Growth

The Logistic Growth 0:08:54

The Logistic Growth Differential Equation

World Population -- 0:10:05

World Population -- exponential growth with constantly changing rates

Population Ecology 0:12:09

Population Ecology

Exponential Growth and 0:48:26

Exponential Growth and Decay (Precalculus - College Algebra 66)

Exponential and Logarithmic 0:22:00

Exponential and Logarithmic Application ( Population Growth and Population Decay)

12 - What 0:36:27

12 - What is Exponential Growth & Decay? (Half Life & Doubling Time) - Part 1

The Logistic Differential 0:15:05

The Logistic Differential Equation for Population Growth: General Solution

Modelling Population Growth 0:24:24

Modelling Population Growth

Geometric & Exponential 0:24:12

Geometric & Exponential Population Growth

Комментарии
Автор

This is an example problem using the population of China in 1980 and 2016 to create an exponential function of the form P(t) = ab^t and then use that function to predict the population in 2030.

Notes:
t = the number of years since 1980
P(t) = the population of China in millions

If you have a ti-84 you can determine the values of "a" and "b" in the P(t) = ab^t by inputting the points (0, 981) and (36, 1380) into L1 and L2 ("stat", edit) and then ("stat", calc, 0:ExpReg ).

SulockMath