filmov
tv
A famous limit
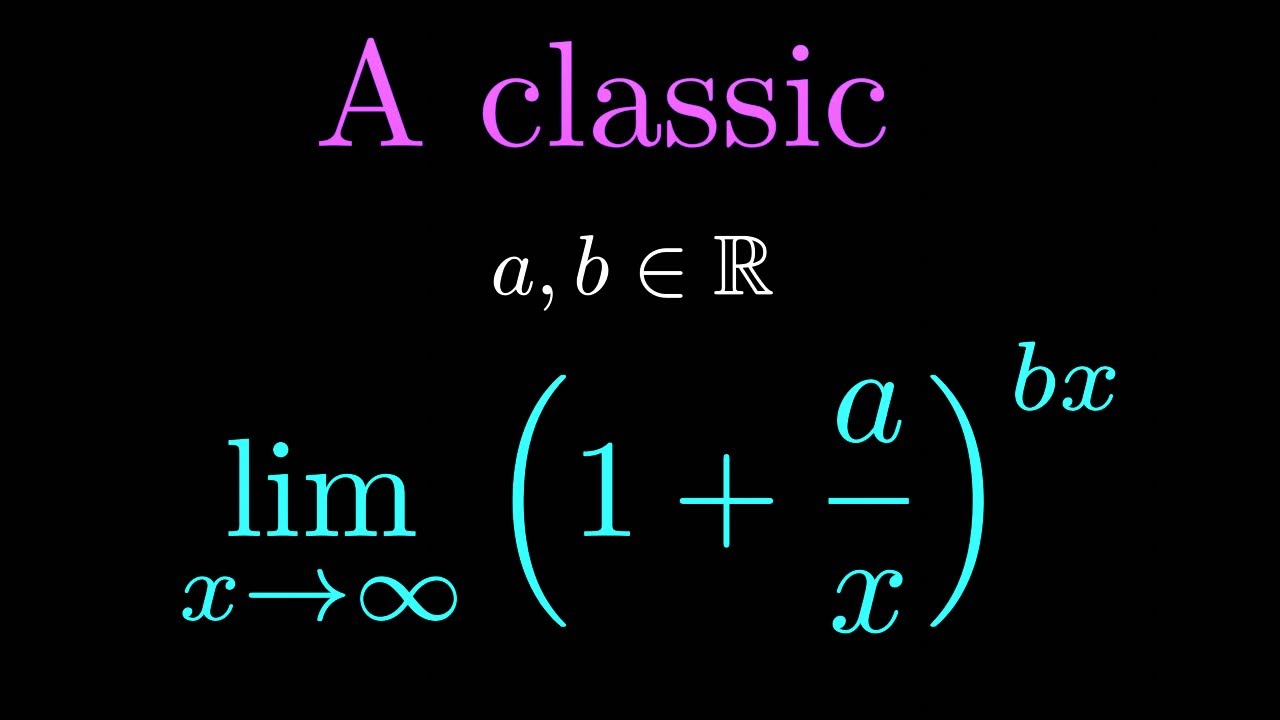
Показать описание
In this video we present a solution to a general limit: (1+a/x)^bx as x approaches infinity.
Thanks for watching I hope you have a great day
Limit of x^x^x as x goes to 0+ :
Limit of (1+1/x)^x as x approaches infinity :
Limit of (x/x+a)^x as x approaches infinity :
Limit of x^x as x goes to 0+ :
I hope you have a great day!
Thanks for watching I hope you have a great day
Limit of x^x^x as x goes to 0+ :
Limit of (1+1/x)^x as x approaches infinity :
Limit of (x/x+a)^x as x approaches infinity :
Limit of x^x as x goes to 0+ :
I hope you have a great day!
This is a very famous limit
Infinite Limit Shortcut!! (Calculus)
The Most Important Limit In Calculus
#limit # how to solve of limits in trigonometric identities, limit x→0, sinx,e²-1/x,x/tanx
A limit that makes calculus teachers die inside #math #tutor #mathtrick #learning #shorts #limits
Solving Limits Mentally #calculus #limit #infinity #rational #mathstricks #shortsviral #shorts
Evaluating A Limit with Tangent and Sine
Limit to ∞ (infinity) of a rational function
Schedule 1 Malware: Increased Stack Limit & Backpack Mods | WARNING
Limit solving (limit at infinity of a rational function)
This Famous Limit Has a Surprising Sibling! || Why sin(x)/x Becomes 0 as x→∞ (Not 1) || HSC LIMIT...
The Shannon Limit - Bell Labs - Future Impossible
Solving a Limit #calculus #mathematics #math #challengingmathproblems #limits
limits laws l limit rules l Basic calculus #calculus #basiccalculus
The Limit (do not use L'Hospital rule)
❖ Lots of Limit Examples, Part 6 ❖
Limit hot trick #shorts #maths #tricks #limit
easiest method to solve limits #maths #subscribe #limit
PUSH IT TO THE LIMIT #scarface
easiest method to. solve limit by L Hospital rule #maths #limit #subscribe
Simple Limit
Limit
Famous limit Question || Olympiad Questions
Limit of a Function at a Point #limits #emsat #emsat_math
Комментарии
 0:00:48
0:00:48
 0:00:51
0:00:51
 0:03:05
0:03:05
 0:00:07
0:00:07
 0:00:07
0:00:07
 0:01:00
0:01:00
 0:00:33
0:00:33
 0:00:33
0:00:33
 0:02:43
0:02:43
 0:01:00
0:01:00
 0:08:12
0:08:12
 0:05:31
0:05:31
 0:00:44
0:00:44
 0:00:12
0:00:12
 0:12:08
0:12:08
 0:12:49
0:12:49
 0:00:14
0:00:14
 0:01:00
0:01:00
 0:00:31
0:00:31
 0:00:49
0:00:49
 0:01:01
0:01:01
 0:00:50
0:00:50
 0:02:12
0:02:12
 0:01:00
0:01:00