filmov
tv
A nonconducting spherical shell, with an inner radius of 4.0 cm and an outer radius of 6.0 cm, has c

Показать описание
A nonconducting spherical shell, with an inner radius of 4.0 cm and an outer radius of 6.0 cm, has charge spread nonuniformly through its volume between its inner and outer surfaces. The volume charge density ρ is the charge per unit volume, with the unit coulomb per cubic meter. For this shell ρ = b/r, where r is the distance in meters from the center of the shell and b = 3.0 µC/m^2. What is the net charge in the shell?
A nonconducting spherical shell, with an inner radius of 4.0 cm and an outer radius of 6.0 cm, has c
A nonconducting spherical shell of inner radius a = 2.00 cm and outer radius b = 2.40 cm has (within
6-85. Electric field and non-conducting spherical shells
A nonconducting spherical shell, with an inner radius of 4.0 cm and an outer radius of 6.0…
In the figure a nonconducting spherical shell of inner and outer radius
A nonconducting spherical shell has charge spread uniformly between its inner and outer surfaces
A nonconducting spherical shell, with an inner radius of 41 cm and an outer radius of 78 cm, has a
The figure shows two nonconducting spherical shells fixed in place
non conducting thick shell |Mustafa Prince
Electrical Potential Conducting Shells
Chapter 22 | Problem 39 | Physics for Scientists and Engineers 4e (Giancoli) Solution
A conducting spherical shell with inner radius a and outer radius b has a positive - 22.42
Field due to uniformly charged thin spherical shell | Gauss law | Physics | Khan Academy
A nonconducting sphere with radius a is concentric with and surrounded by a conducting spherical
Electric Potential of a Conducting Sphere
A nonconducting sphere with radius a is concentric with and surrounded by a conducting spherical ...
The figure shows a spherical shell with uniform volume
Electrical Potential of a Conducting Sphere (or Shell)
electric field due to a non conducting spherical shell
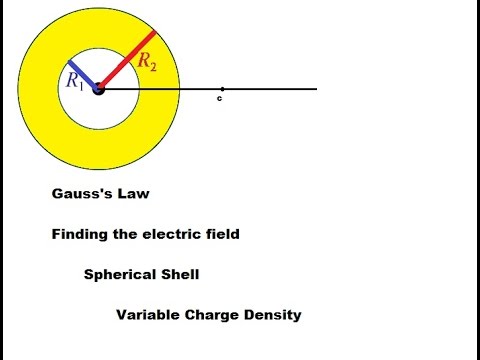
Gauss's Law for electric field in a spherical shell. Variable charge density.
Gauss's Law for electric field in a spherical shell. Variable charge density.
Electrostatics||Field Due to Conducting & Non Conducting Spherical Shell (By Mohit Sir)
A thin nonconducting spherical shell of radius 6 cm carries a uniform surface charge density ? = 13…...
A charged particle is suspended at the center of two concentric spherical
Комментарии
 0:03:45
0:03:45
 0:07:45
0:07:45
 0:05:22
0:05:22
 0:00:33
0:00:33
 0:11:18
0:11:18
 0:04:19
0:04:19
 0:05:17
0:05:17
 0:07:55
0:07:55
 0:11:04
0:11:04
 0:20:42
0:20:42
 0:09:49
0:09:49
 0:08:59
0:08:59
 0:06:42
0:06:42
 0:04:15
0:04:15
 0:08:08
0:08:08
 0:07:12
0:07:12
 0:10:39
0:10:39
 0:17:50
0:17:50
 0:00:39
0:00:39
 0:11:57
0:11:57
 0:02:51
0:02:51
 0:13:17
0:13:17
 0:00:33
0:00:33
 0:06:04
0:06:04