filmov
tv
When is This Fraction an Integer?
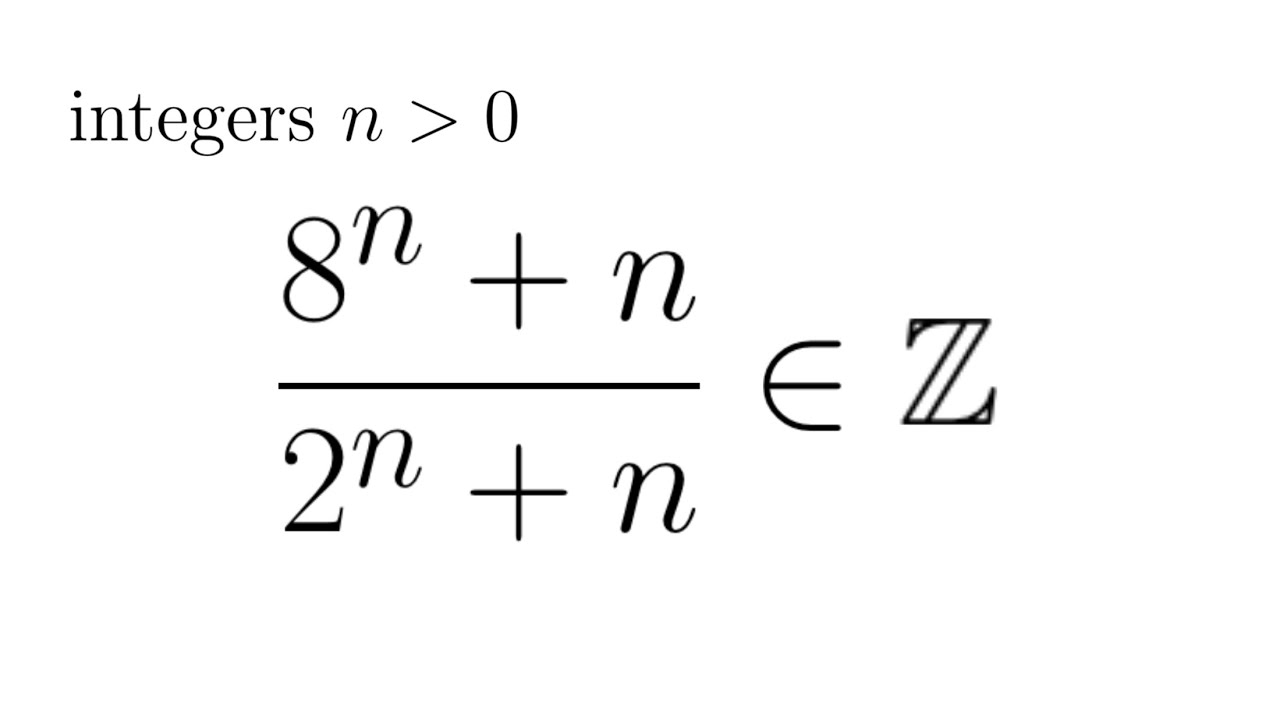
Показать описание
When is This Fraction an Integer?
When is This Fraction a Cube?
Did you know this Fraction Tricks #math #mathematics #mathstricks #maths #mathhacks
How to Calculate ANY Fraction Easily!
How To EASILY Solve This Fraction/Exponent Problem | Math Tips
How to Find a Fraction of a Whole Number | Fractions of Whole Numbers
Fraction Trick
Find an equivalent fraction #shorts
A2 Pure Mathematics - 4B Binomial Expansion with negative & fractional indices
What fraction is the shaded part? Each equal part is what fraction? #math #youtube #shorts
Equivalent fractions | fraction tricks |#equivalent #fraction#fractions #shorts#mathstricks#ytshorts
What is a Fraction
How to Simplify a Fraction over a Number and a Number over a Fraction
Turning Mixed Number Into Improper Fraction - Math Hacks
Hack for all ages | convert mixed fraction to improper fraction #math #shorts #mathematics #maths
Converting Mixed Number Into Improper Fraction #fractions #math #silentmath
Subtraction of Mixed Fraction Tricks || @Sky Struggle Education #short
Trick For Fraction LCM(see description)
Fractions trick | Fraction tricks #fraction #fractions #mathtricks #mathstricks #shorts
Easy fraction trick you should know
01 - What is a Fraction? - Definition & Meaning - Part 1 - Numerator, Denominator & More.
Converting Improper Fraction Into Mixed Number (11/7 = ?) #fractions #mathtutor #silentmath
How to Add Fractions / Fraction Addition / Adding Fractions / Learn Addition of Fractions
IMPROPER FRACTION question#short #viral #youtubeshorts#maths
Комментарии
 0:07:52
0:07:52
 0:09:06
0:09:06
 0:01:00
0:01:00
 0:12:29
0:12:29
 0:00:25
0:00:25
 0:06:12
0:06:12
 0:00:08
0:00:08
 0:01:00
0:01:00
 0:09:04
0:09:04
 0:00:27
0:00:27
 0:00:07
0:00:07
 0:02:51
0:02:51
 0:05:51
0:05:51
 0:00:10
0:00:10
 0:00:23
0:00:23
 0:00:43
0:00:43
 0:00:11
0:00:11
 0:00:17
0:00:17
 0:00:13
0:00:13
 0:04:48
0:04:48
 0:18:49
0:18:49
 0:00:44
0:00:44
 0:08:46
0:08:46
 0:00:23
0:00:23