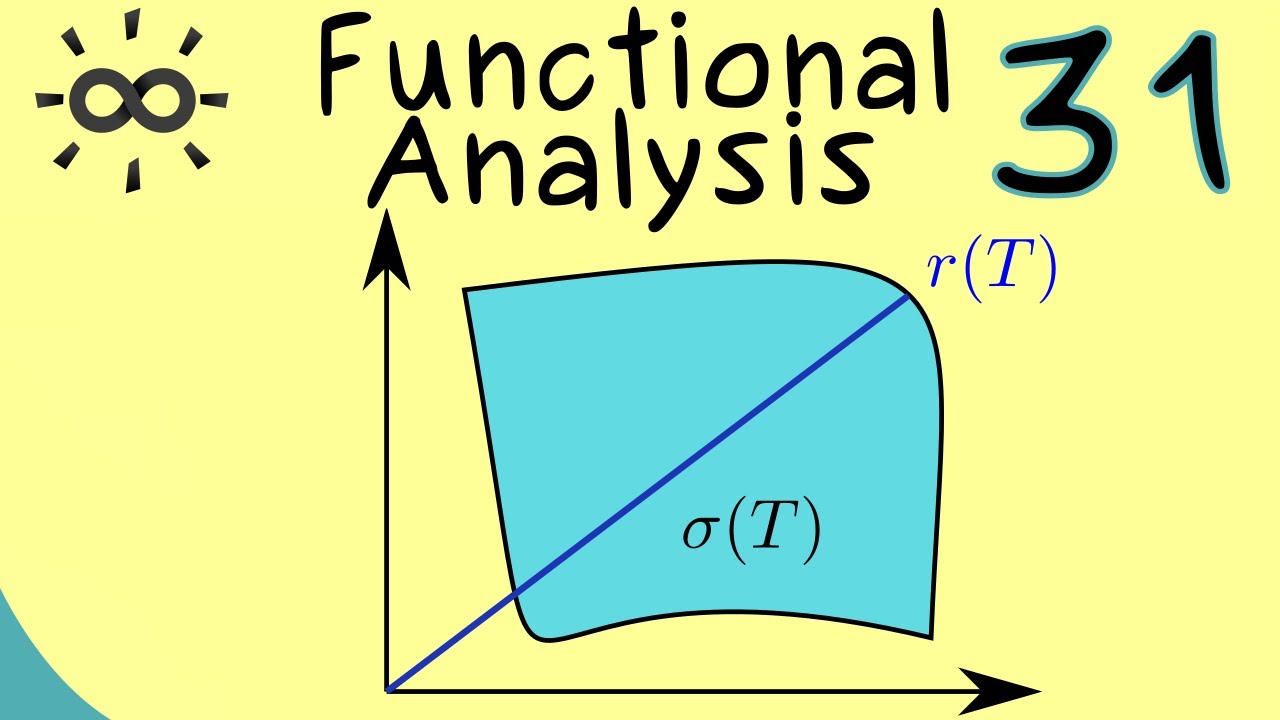
Functional Analysis 31 | Spectral Radius

Please consider to support me if this video was helpful such that I can continue to produce them :)

🙏 Thanks to all supporters! They are mentioned in the credits of the video :)

This is my video series about Functional Analysis where we start with metric spaces, talk about operators and spectral theory, and end with the famous Spectral Theorem. I hope that it will help everyone who wants to learn about it.

x

#FunctionalAnalysis
#VectorSpaces
#Mathematics
#LearnMath
#calculus

I hope that this helps students, pupils and others. Have fun!

(This explanation fits to lectures for students in their first and second year of study: Mathematics for physicists, Mathematics for the natural science, Mathematics for engineers and so on)

[Ghetto_Bird]

You are such a knowledgeable mathematician, truly outstanding.

[FloriUchiha]

Judging from your explanation in your videos, you have a very deep understanding of the topic and you helped me alot to understand functional analysis. I would really love to see some videos about the applications on elliptic PDE's and also about the Sobolev space (maybe also about the Hölder space), since this was the most difficult part for me to understand. Thank you for the great videos anyway!

[seneketh]

Thank you so much. I will need a long time to unpack your videos.

[jiqingjiang]

At the end of the vedio, I cannot see how Hahn Banach theorem applys, could you give some hints? Thanks!

[StratosFair]

Wow, what a nice proof ! Btw, I have a question which might be outside the scope of this course : judging by your drawings, it seems the spectrum has infinite (uncountable) cardinality. Is it always the case ?

[养兔大户]

Really really thank you ! could you please recommend any textbook i can refer to about functional analysis?

[metalore]

It appears when you write T^-2, you mean the linear operator formed by multiplying T inverse with T inverse. I am starting to understand you can work with exponents of functions the same way as with numbers. In particular in the Taylor series you are applying other exponents to change the ^-1 exponent which is normally used as inverse notation. Do you have videos that delve into this? Does this only work with linear operators?

[StratosFair]

What about the last bit of proving that the spectral radius is the limit of a sequence of operator norms ? This doesn't seem to follow directly from the two other results 🤔
Any hints or reference ?

[miguelriesco]

I’d like to understand why the function f_{l} is holomorphic. I supoose you can use the continuity of l and the series expansion of the resolvent(?)

[dyy]

This is an excellent video and the proof involves a lot of interesting knowledge. Would be even better if elaborate why the composition of linear functionals and analytic functions is still analytic :)

[abublahinocuckbloho]

care to explain why lambda is not in the spectrum?