Implement A Sudoku Solver - Sudoku Solving Backtracking Algorithm ('Sudoku Solver' on LeetCode)

📹 Intuitive Video Explanations
🏃 Run Code As You Learn
💾 Save Progress
❓New Unseen Questions
🔎 Get All Solutions

Question: Implement a Sudoku solver. (a classic Sudoku board is 9x9)

The Rules of Sudoku:

We are working with numbers 1 thorugh 9.

Each number can only appear once in a:

Row
Column
And one of the 3 x 3 subboxes

Approach 1 (Brute Force)

Try every possible assignment to empty entries and then at the end validate if the sudoku board is valid or not.

With no constraints, given a 9x9 board we have at max 81 spaces where in each space we can place the number 1-9 (but on a normal board many spaces will already have a number before we even start solving)

This means that there are 9^81 total arrangements of the board (as a loose upper bound). This is 1.9662705 * 10 ^ 77 boards just for a 9 x 9 board.

This would take too long.

Approach 2 (Apply The Constraints)

The backtracking approach.

We can traverse and place an entry in empty cells one by one.

We then check the whole board to see if it is still valid.

If it is we continue our recursion.

If it is not we do not even follow that path.

When all entries have been filled, we are finished.

The 3 Keys To Backtracking:

Our Choice

What we place in an empty cell that we see.

Our Constraints

Standard Sudoku constraints. We cannot make a placement that will break the board.

Our Goal

Place all empty spaces on the board. We will know we have done this when we have placed a valid value in the last cell in our search which programmatically will be the bottom right cell in the 2D matrix.

Validating Placements Before We Place Them

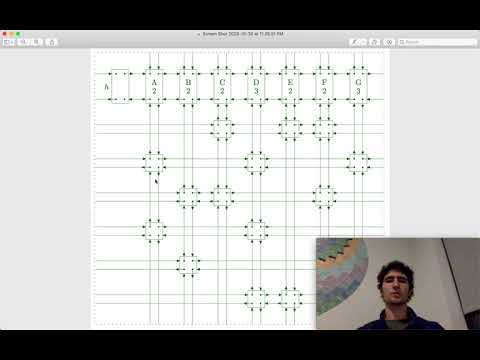
INSIGHT: We could traverse every row, column, and 3x3 subgrid to perform validation but at every decision point we know that we are adding onto a grid that is already valid.

So we just check the row, column, and subgrid of the item that has been added.

Whenever backtracking we know that every decision that we made stayed within the constraint that we started with being that the board was valid.

Complexities

Since Sudoku is traditionally 9x9 we can't really discuss complexities because nothing can scale.

Solving Sudoku generalized to n x n boards is a NP-Complete problem so we know for sure that our time complexity is exponential at the very least.

++++++++++++++++++++++++++++++++++++++++++++++++++

++++++++++++++++++++++++++++++++++++++++++++++++++

This question is number 16.9 in "Elements of Programming Interviews" by Adnan Aziz, Tsung-Hsien Lee, and Amit Prakash.

[BackToBackSWE]

Table of Contents:

The Problem Introduction 0:00 - 0:44
More Information On The Problem 0:44 - 1:52
The Brute Force Approach (Complete Search) 1:52 - 3:09
The Backtracking Approach (3 Keys To Backtracking) 3:09 - 3:30
Our Choice 3:30 - 4:18
Our Constraints 4:18 - 6:28
Our Goal 6:28 - 7:41
Time & Space Complexity 7:41 - 9:11
Conclusion 9:11 - 9:34

The code for this problem is in the description (with many comments for teaching purposes).

[lilzjay]

Hey bro, you are not yelling. I can feel a strong passion from your voice!

[johnskeff]

Where is the code?? There is NO code in the description!

[bisann]

thank u so much!! but where's the code exactly?

[somerandomguy]

I actually prefer the yelling and passionate approach. You’re the best!

[anshulabhinav]

I was hoping you would do a dry run on the example input board, just like you do for most of your other videos. That really helps in firming the understanding, more than the code.

[shivankchaturvedi]

U aren't yelling this shows ur passion towards the problem don't change the tone

[steelcube]

What happen when the program has picked a number for a cell and later needs to change it due to other cells constrains? I mean it could be valid at the time it picks a number but may need to be changed later?

[algorithmimplementer]

If you keep this up, as you started at the very young age at college, I am sure you will go very far. :)

[sobowaleolamide]

Nice solution. I followed your approach but I did a bit of an update on it. Instead of checking everytime if a character can be placed in row or column or region at O(n^2) runtime, you can do that in constant time by saving keeping track of the content of each region, each row, and each column, then you can backtrack on it. after trying any character.

[joshstafford]

When did you actually explain backtracking though...

[vanyastaleva]

Hmmm, am I the only one who can't find the code? He said that in the description box there is a link to the code

[xinzhang]

very clear to illustrate the hard part of this problem. Great job man, you deserve more subs, and keep going!

[gurtagel]

One question I have is how we can figure out which valid value to use. For example, when we are looking at the second blank spot, you put a 2 there and proceed with the assumption that it is valid. However, how did you know that the second blank could not be a 6 instead. There are no 6's in that row, column, or sub-matrix?

[xiuwenzhong]

cannot believe it, I first search Sudoku Solver in youtube, I did not found your video. Then I watch other guys video which make me confused but I saw a leetcode link under that video comments. Then in the leetcode discuss, I saw your video link, that's how I found it.

[vibhoresrivastava]

Great explanation. I've checked out a lot of your videos past few days. You are doing a great job. Wish my algorithms professor was like this.

[AreeshaTariq-rl]

3:50 row, column traversal
4:40 we cannot break the board (dont do an n^2 check)
6:30 how do i know im finished

[practice]

your explanation is best, best teacher ever

[mihailovasic]

Hey mate, love your videos, but I have a question about the line 35:
board[row][col] = EMPTY_ENTRY;
why does it work with it and why doesn't it work without it? I mean, you set a value for a cell, and then you set it to EMPTY_ENTRY, why?

[lizziedaffofil]

Loved it more when you are loud:) such energy is contagious!