critical numbers of an absolute value of a function (with quadratic inside)

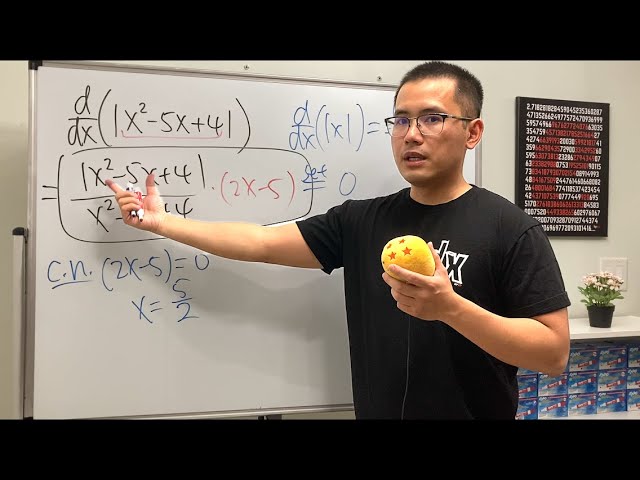
Показать описание

Calculus 1: critical numbers of an absolute value of the function (with quadratic inside)

------------------
10% off with the code "WELCOME10"
------------------
math, but FAST!

Рекомендации по теме

Комментарии

I am not first
I am not last
But when bprp posts
I do click fast

antonlindemer

Generally speaking, for an arbitrary polynomial p(x), the first derivative of |p(x)| is [|p(x)|/p(x)] p'(x), so any point x such that p(x) = 0 will be not differentiable if such x does not make p'(x) = 0. Nevertheless, if x satisfies both conditions p(x) = 0 and p'(x) = 0, we get x has a winding number >= 2, a.k.a. a repeated root of p(x), then by the limit definition, we get that the first derivative of |p(x)| at x is 0 regardless which approach we use, and graphically we can see that the polynomial is smooth at such x value. (It is easier to visualize that if we keep both the domain and the codomain in the real set although it still holds by bringing both into the complex world.) But again, regardless of whether the roots of |p(x)| are differentiable, we should always keep in mind that all those roots are relative minimum (a.k.a. local minimum) since |p(x)| >= 0 provided that there is no other x value in the domain around the roots giving us |p(x)| < 0.

kobethebeefinmathworld

So d/dx (ax² - bx + c ) taking the deratives ( 2ax - b ) = 0
2ax = b
X = b/2a? ( Turning point)???

jx_was_here

Hella helpful, abs values are very simple in theory but when it comes down to solving problems with it it gets complicated fast

piupolino

Can I do d/dx |x| = x/|x| ??
Are there any advantages to put the absolute value in the numerator?

Drestanto

Which value of n
1 to ∞ ∫ ( {x} / (x)^(n+1) ) dx question solution is =( 1/(n+1) )
Where {x} = ( x - floor(x) )
Please make a video on this question 🥺🙏.

numberandfacts

He’s growing impatient with the slow students in this video

robberbarron

evaluate: integration 2^(2^(2^x)) * 2^(2^x) * 2^x dx
This question is very hard 👆👆
you will never be able to solve

balkrishna

critical numbers of an absolute value of a function (with quadratic inside)

Finding Critical Numbers

Find the critical values of an absolute value function

critical numbers of an absolute value of a function (with quadratic inside)

Critical Numbers for Absolute Value - Find the critical numbers of the function g(t) = |3t - 4|

How to Find the Critical Numbers and Relative Extrema from the Graph in Calculus

Finding Absolute Maximum and Minimum Values - Absolute Extrema

Steps to Find Absolute Maximum and Minimum Using Critical Numbers

Critical numbers and relative extrema for piecewise functions

Maths Marathon🔥 | Integral Calculus | Part 2 | Top 100 PYQs | JEE Main 2025 | Bhoomika Ma'am

Finding the Critical Numbers and Absolute Extrema (Exponential Function)

Finding the Critical Numbers and Absolute Extrema (Linear Function)

Find Critical Number Extreme Maximum and Minimum Value for Absolute Function

Critical points introduction | AP Calculus AB | Khan Academy

CRITICAL NUMBERS AND CRITICAL POINTS - How to find critical numbers of a function and with a graph

CRITICAL Numbers!!!

Local and Absolute Max/Min and Critical Points/Numbers

Finding the Critical Numbers and Absolute Extrema (Rational Exponent)

Finding the Critical Numbers of the Function f(x) = x^(2/3)

Finding Critical Numbers of polynomials, absolute value, and fractions

How to find Critical Numbers (Worked Examples)

Find the critical numbers of the function g(t) = |3t -4|

Finding Critical Numbers Example 1

Critical Numbers and Relative Extrema from Graph Simple Example

How to find CRITICAL NUMBERS 🥸😼 #shorts #criticalnumbers #criticalvalues #calculus