Given the first term and common ratio, find the explicit formula of the geometric sequence

Показать описание

👉 Learn how to write the explicit formula for a geometric sequence. A sequence is a list of numbers/values exhibiting a defined pattern. A number/value in a sequence is called a term of the sequence. A geometric sequence is a sequence in which each term of the sequence is obtained by multiplying a pre-determined value, called the common ratio, to the preceding term.

The explicit formula for the nth term of a geometric sequence is given by An = ar^(n - 1), where a is the first term, n is the term number and r is the common ratio.

Organized Videos:
✅ Sequences
✅Sequences | Learn About
✅Determine The First Five Terms of The Arithmetic Sequence
✅How to Write The Formula for a Arithmetic Sequence
✅Find the nth Term of an Arithmetic Sequence
✅Find the First Five Terms of a Geometric Sequence
✅How to Write The Formula for a Geometric Sequence
✅Find the nth Term of a Geometric Sequence
✅How to Determine Arithmetic or Geometric Sequence
✅Find the First Five Terms of a Sequence
✅How to Write The Formula for a Sequence
✅Find the nth Term of a Sequence
✅How to Simplify Factorials
✅Recursive Sequences
✅Prove the Sum by Induction
✅Find the Given Term of Binomial Expansion
✅Binomial Expansion | Learn About
✅How to Expand a Binomial

Connect with me:

#sequences #brianmclogan

Рекомендации по теме

Комментарии

Thanks alot man saved my math grade and my highschool career

iansmith

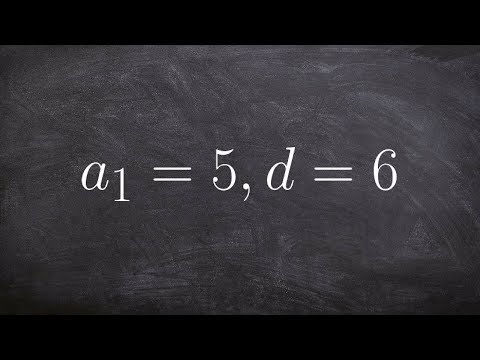Given the first term and common ratio, find the explicit formula of the geometric sequence

Given the first term and the ratio find the nth term of a geometric sequence

Given second and fifth terms as -2, 7, respectively, find first term and recursive rule for nth term

Given the first term and ratio find the first four terms of a geometric sequence

Given the first term and ratio determine the first five terms of a geometric sequence

Given the first term and the difference determine the rule for a arithmetic sequence

Given the first term and ratio find the nth term of a geometric sequence

Given the first term and common ratio, find the explicit formula of the geometric sequence

Geometric Sequences: Find First Term and Common Ratio given Sum to nth term and Infinity

Given the ratio and first term of a geometric sequence write the rule for nth term

Arithmetic Progression - 6. Finding nth term of an AP given the first term and common difference

Given the first value and d use the formula to find the first four terms of a sequence

Arithmetic Progression - 4. Finding first term and common difference for given AP

Arithmetic Sequence given first term and common difference | General nth Term

Given first term and a or d find the nth term of a sequence

Given fourth and seventh term of geometric sequence find first term, common rule, explicit rule

Example Finding a Partial Arithmetic Sum Given First Term and Common Difference

Find the First Term and the Common Difference given Nonconsecutive Terms of an Arithmetic Sequence

Finding the first 5 terms of the sequence given the nth term

Find The Nth Term of an Arithmetic Sequence Given The First Term and Common Difference

Number of Terms of the Arithmetic Sequence Given the First Term, nth Term, and Common Difference

Find the first several terms of a sequence with given two terms

Arithmetic Progression - 3. Finding first few terms of AP given first term and common difference

When given two values of a sequence find the first term

Find the 7th term of a geometric sequence given the first term and the 4th term (find r first)